Статистические ансамбли

Рассмотрим системуА, с которой мы производим какие-то опыты или наблюдения *). Часто результат данного одиночного опыта не может быть предсказан с полной определенностью либо по прин­ципиальным соображениям, связанным с внутренней сущностью явления **), либо потому, что доступная нам информация недоста­точна для такого предсказания. Однако, если результат данного

*) Акт наблюдения можно трактовать как опыт, результат которого совпадает с результатом наблюдения. Поэтому нет необходимости проводить различив -между опытом и наблюдением.

**) Такая ситуация имеет место, например, в квантовой, механике, где результат измерений, совершаемых в микроскопической системе, не может быть предсказан с полной однозначностью.

одиночного опыта и не может быть указан, все же иногда можно сделать весьма важные выводы о результатах большого числа идентич­ных опытов. В таком случае мы говорим о статистическом описании' системы и 'используем для такого описания методы теорий вероятностей. Это описание можно выполнить, следующим образом.

Вместо того чтобы сконцентрировать наше внимание на данной системеА, которая нас интересует, рассмотрим набор систем, (ан­самбль в терминологии, принятой в статистике), состоящий из большого числа N «одинаковых» систем. В принципе Nможно предста­вить себе сколь угодно большим . Системы предполагаются «одинаковыми» в том смысле, что каждая из них удовлетворяет тем же условиям, которым удовлетворяет система А. Это значит, что мы считаем каждую из систем приготовленной по тому же рецепту и подвергнутой тому же опыту, что и система А. Мы можем теперь спросить, в какой части случаев будет иметь место данный конкретный результат опыта? Чтобы быть точными, нам следует иметь возможность каким-то образом пронумеровать или обозначить различные и исключающие друг друга результаты опыта. (Полное число таких возможных результатов может быть конечным или бесконечным.) Обозначим теперь некоторый определенный результат опыта индексом rи предположим, что из N систем» образующих наш ансамбль, N_rсистем дали такой результат. Тогда отношение

 

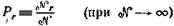
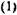
называется вероятностью появления результата r. Если Nочень велико, то можно ожидать, что повторение того же опыта с данным ансамблем приведет к тому же отношению Р_r. Поэтому отношение (1) дает однозначный результат в пределе, кргдаN может быть сделано произвольно большим.

Это рассуждение показывает, что для измерения вероятности любого возможного результата опыта с данной системой необходимо повторить этот одыт на большом числе одинаковых систем *). Несмотря на то, что результат данного частного опыта нельзя предсказать, статистическая теория позволяет предсказать вероятность появления каждого из возможных результатов опыта. Предсказанные вероятности можно сравнить с вероятностями, измеренными на опыте с ансамблем одинаковых систем.

Рассмотрим несколько конкретных примеров.

Бросаниемонетыилиигральнойкосети.Пусть наш опыт заключается в бросании монеты. Он имеет два возможных исхода: «орел» или «решка». В принципе, результат этого опыта может быть полностью предсказан, если нам известно все об условиях бросания монеты и об ее взаимодействии с поверхностью стола. Для такого предсказания необходимо произвести сложные вычисления,

*) Если состояние системы не зависит от времени, то с равным успехом можно один и тот же опыт-повторить Nраз над одной данной системой. При этом, разу­меется, нужно быть уверенным, что в начале каждого опыта система находится в одном и том же начальном состоянии.

основанные назаконах классической механики. На самом же деле мы не распола­гаем полными данными об условиях бросания монеты и не можем поэтому пред­сказать результат данного бросания. (Даже если бы мы имели полную информацию о начальных условиях и могли произвести все вычисления, нас не удовлетворил бы столь сложный способ получения результата.) Статистическая формулировка этого опыта очень проста. Достаточно рассмотреть ансамбль, со­стоящий из очень большого числа одинаковых монет. Бу­дем бросать эти монеты одинаковым приемом и подсчиты­вать число случаев выпадения «орла» или «решки» *). Доля таких случаев дает соответственно измеренную вероятность рпоявления «орла» или вероятность qпоявления «решки». Статистическая теория должна уметь предсказывать эти вероятности. Например, если центр масс монеты совпа­дает с ее геометрическим центром, то из соображений сим­метрии следует, что в законах механики не содержится ни­чего, что позволило бы различить «орла» и «решку». В та­ком случае половина экспериментальных результатов долж­на дать «орла», другая половина «решку», поэтому p=q=¹/₂. Сравнение с опытом может подтвердить или опровергнуть такую теорию. Например, если «орел» появляется чаще «решки», мы будем считать, что теория неверна в той части, которая предполагает совпадение центра масс с геометрическим центром.

 

Рассмотрим теперь несколько более сложный опыт бро­сания N монет. Бросание каждой монеты имеет два возмож­ных исхода, поэтому бросание N монет приводит к появле­нию 2Х2Х ... X2=2^Nрезультатов **). Статистическая формулировка этого опыта заключается в том, что вместо одного набора из N монет мы рассматриваем ансамбль, состоящий из Nтаких наборов по N монет в каждом, и над каждым набором производим одинаковый опыт. Вопрос, который может представлять интерес при таком одинако­вом бросании наборов монет, заключается, например, в вероятности появления одного из 2^Nвозможных резуль­татов опыта. Примером менее детального вопроса является нахождение вероятности того, что л монет из нашего набо­ра выпадут «орлом», а остальные (N— п) монет выпадут «решкой».

Задача о бросании набора из N одинаковых игральных костей имеет, конечно, аналогичный характер. Единствен­ное различие связано с тем, что бросание любой кости дает шесть возможных исходов, в зависимости от того, какая из шести граней смотрит вверх.

Исход некоторого опыта или результат наблюдения часто удобно обозначать простым словом случай. Заметим, что вероятность реа­лизации данного случая существенным образом зависит от доступ­ной нам информации относительно рассматриваемой системы. Дейст­вительно, эта информация определяет наш статистический ансамбль, состоящий из систем, свойства которых совпадают со свойствами рас­сматриваемой системы. Поясним это на следующем примере.

*) Мы можем поступить иначе, бросай Nраз одну и ту же монету и подсчи­тывая случаи «орла» и «решки».

**) В частном случае N=4 возможны 2⁴= 16 возможных результатов. Ониперечислены в табл. 1.1 (стр. 20), где букву Л можно принять за «орла»; а букву Пза «решку».

Пример.Нас интересует следующий вопрос: какова вероятность того, что житель Соединенных Штатов окажется в больнице в возрасте между-23 и 24 го­дами. В этом случае мы должны рассмотреть ансамбль, состоящий из большого числа жителей Соединенных Штатов, и определить, какая их доля между 23 и 24 го­дами жизни окажется в больнице. Предположим что существует дополнительное условие, заключающееся в том, что это женщины. Ответ на наш вопрос изменится, так как теперь мы должны будем рассмотреть ансамбль женщин -жительниц Соединенных Штатов и определить, какая их часть оказалась в больнице в возрасте от 23 до 24 лет. (Очевидно, что благодаря деторождению женщины этого возраста будут находиться в больнице ча­ще, чем мужчины.)

return false">ссылка скрыта

Системы с большим количеством частиц. Рас­смотрим макроскопическую системуА, состоящую из многих частиц. Такой системой может быть, например,, идеальный газ, содержащий N мо­лекул, или система из N спинов, или жидкость, или кусок меди. Ни в одном из этих случаев мы не можем предсказать поведение каждой части­цы, образующей систему, к тому же такое пред­сказание не представляет интереса *) и поэтому следует обратиться к статистическому рассмот­рению системы А. Вместо того чтобы исследовать одну такую систему, рассмотрим ансамбль, со­стоящий из большого числа N систем, аналогичных системе А. Чтобы высказать некоторые статистические утверждения о нашей системе в момент времени t, мы произведем в этот мо­мент времени наблюдения над N системами. Это даст нам вероятность P_r(t) наблюдения определённого результата опыта в момент вре­мениt. Предполагаемая процедура станет зна­чительно более ясной, если мы вообразим, что имеем фильмы, на которых снята каждая система нашего ансамбля. Поведение любой, скажем, R-й, системы ансамбля в зависимости от времени мы можем теперь изучать, рассматривая R-й фильм (для этого нужно смотреть соответствующую горизонталь на рис. 2.3). С другой стороны, для получения каких-то вероятностных утверждений о системе в некоторый момент времени t необходимо рассмотреть те кадры на всех фильмах, которые относятся к определенному моменту времени t(для этого нужно изучить кадры, расположенные на рис. 2.3 вдоль вертикали, и сосчитать долю кадров, на которых обнаружен интересующий нас результат опыта).

Мы говорим, что свойства статистического ансамбля не зависят от времени, если число систем, отвечающих данному случаю, одно и то же в любой момент времени (или, что то же самое, есливероятность появления любого данного случая в ансамбле не зависит от времени). Тем самым статистическое описание позволяет дать очень ясное определение понятия равновесия: изолированная макроскопическая система находится в равновесии, если - свойства статистического ансамбля из таких систем не зависят от времени.

 

*) В точном квантовомеханическом описании системы нестатистнческие пред­сказания невозможны принципиальна.При классическом описании точные пред­сказания о системе требуют знания положения и скорости каждой частицы в не­который момент времени. Такая информация нам недоступна.

 

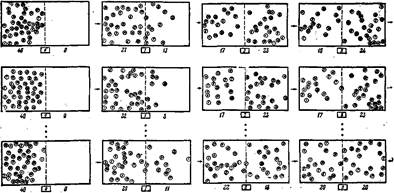
Ряс. 2.3. Полученные с помощью вычислительной машины рисунки образуют статистический ансамбль систем. Этот ансамбль должен отразить поведение системы, состоящей из 40 частиц, заключенных в ящик. Доступная нам информация о системе заключается в следующем: в начальный момент временя (кадрi=0) все частницы находятся в левой половине ящика.но ничего больше об их положенияскорости мы не знаем. Чтобы проследить эволюцию во времени R-й системы ансамбля, нужно рассмотреть горизонтально расположенные R-м ряду кадрыi=0, 1, 2, . . . Чтобы высказать какие-нибудь статистические утверждения о системе в момент времени, отвечающий iму кадру, необходимо рассмотреть расположенные по вертикали i-е кадры и произвести счет числа систем, необходимый для определения вероятности.

 

 

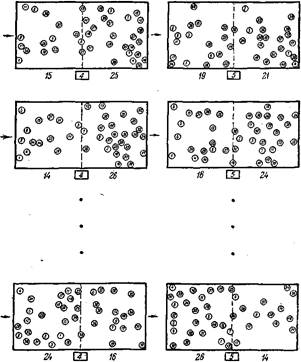
Рис. 2.4. Продолжение рис. 2.3. Теперь, когда прошло достаточное время, ансамбль является независимым от времени. Это означает: что система достигла состояния равновесия.

Пример.Рассмотрим идеальный газ, состоящий из Nмолекул. В некото­рый начальный момент времени t, сразу после того, как убрана перегородка, все молекулы этого газа находятсяв левой половине сосуда. Каким образом можно произвести статистическое описание поведения газа в последующие моменты вре­мени? Мы должны рассмотреть ансамбль, состоящий из большого числа аналогич­ных сосудов с газом, в каждом из которых в начальный момент времени все молекулы.находятся в левой половине сосуда. Такой ансамбль схематически показан на рис. 2.3. Затем мы должны исследовать наш ансамбль в определенный момент времени t, с тем чтобы получить ответ на интересующие нас вопросы. Например, если сосредоточить внимание на определенной молекуле, то нас может интересо­вать, какова вероятность р(t) того, что эта молекула находится в левой части со­суда, или вероятность q (t) того, что она находится в его правой части, или, напри­мер, какова вероятность Р (п, f), что в данный момент п из общего числа N молекул оказались в левой части сосуда. Мы знаем, что в начальный момент времени t_aвероятностьр(t₀) = 1 и q (t₀) =0. Точно так жеР(N, t₀) = 1 и Р (п, t₀) = 0 для n≠N. С течением времени эти вероятности меняются до тех пор, пока молекулы окажутся равномерно распределенными по объему сосуда, так что р = q= ¹/₂ . После этого ве­роятности не меняются во времени, т. е. ансамбль становится независимым от вре-мени и система достигает равновесия (рис. 2.4) *). Состояние, при котором поведе­ние системы не зависит от времени, оказывается особенно простым. Действительно, в этом случае задача о газе, состоящем из Nмолекул, аналогична рассмотренной выше задаче о наборе из N монет. В частности, вероятность рнахождения молекул в левой части сосуда совпадает с вероятностью того, что брошенная монета выпадает «решкой»; аналогично, вероятность qнахождения молекулы в правой части сосуда совпадает с вероятностью выпадения «орла». Точно так же, как в примере с моне­тами, эти вероятности не зависят от времени и р = q= ¹/₂

Замечание.В главе 1 [см. уравнение (1.4)] мы вычисляли различные вероятности, рассматривая одну-единственную систему. Такой метод годится для специального случая системы, находящейся в равновесии. Так как ансамбль таких систем не зависит от времени, то большое число последовательных наблюдений над одной системой эквивалентно большому числу одновременных наблюдений над сис­темами ансамбля. Другими словами, предположим, что мы взяли фильм, на кото­ром заснято поведение системы за время т, и разрезали его на N равных частей, каждая из которых длится т₁=т/N(т₁ достаточно велико, чтобы поведение системы на одном куске фильма можно было считать независимым от ее поведения на смеж­ных кусках). В этом случае набор из Nразрезанных фильмов для данной системы будет неотличим от набора Nфильмов, снятых для систем ансамбля в течение ин­тервала времени т₁.