Спектральное представление непериодических сигналов.
В теории спектрального представления непериодических (импульсных) сигналов используют искусственный прием, формально заменяя такие сигналы периодическими с бесконечно большим периодом следования Т→∞.
Положим, что некоторая заданная функция S(t) аналитически описывает одиночный импульсный сигнал конечной длительности. Мысленно дополнив его такими же импульсными сигналами, следующими с некоторым интервалом Т, получим периодическую последовательность аналогичных импульсов Sn(t)= S(t+nT).
Для того чтобы вне искусственного интервала 0, Т исходный сигнал был равен нулю, необходимо увеличить период повторения импульсов. В пределе, при увеличении периода и Т→∞, все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность S(t) вновь станет одиночным импульсом. В этом случае выражения (1.9.), (1.10) по-прежнему должны сохранять свой смысл, однако угловая частота Ω=2π/Т теперь будет стремиться к нулю, и ее придется заменить бесконечно малой величиной dω. Далее, произведение nΩ при Т→∞., очевидно, может принимать любые значения и является непрерывной функцией n. Поэтому nΩ следует рассматривать как текущую частоту ω, изменяющуюся от -∞ до +∞. Легко заметить, что при увеличении периода следования импульсов Т линейчатый спектр будет все более плотным. В предельном случае, когда Т→∞., равные расстояния между спектральными линиями уменьшатся настолько, что спектр станет сплошным, а амплитуда отдельных спектральных составляющих окажутся бесконечно малыми.
С учетом последних соотношений коэффициент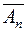 
для бесконечно большого интервала разложения будет равен
где
(1.29)
Отсюда вытекает, что при вычислении S(t) вместо суммирования дискретных значений 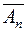ejnΩt в (1.9) необходимо складывать бесконечно малые величины d 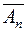(ω)ejωt с частотой, изменяющейся непрерывно. Другими словами, ряд (1.9) превращается в интеграл
. (1.30)
Выражения (1.29) и (1.30) представляют собой прямое и обратное преобразование Фурье.
Итак, из равенств (1.29) и (1.30) видно, что любую непериодическую функцию S(t) можно представить в виде бесконечного множества гармонических составляющих, частоты которых образуют непрерывное множество значений от -∞ до +∞.
Совокупность гармоник, как известно, составляет спектр заданной функции S(t). В рассматриваемом случае каждая гармоника имеет бесконечно малую комплексную амплитуду. Поэтому в качестве спектральной характеристики процесса используется функция 
, называемая спектральной плотностью непериодической функции S(t). Она определяет соотношение между комплексными амплитудами гармоник в спектре.
Если S(t) отлична от нуля на конечном интервале, спектральная плотность ее совпадает со спектральной функцией, ранее введенной в теории рядов.
Спектральная плотность есть функция комплексная. Из выражения (1.29) видно, что
(1.31)
где
(1.32)
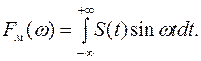(1.33)
Модуль спектральной плотности равен
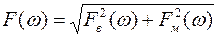. (1.34)
и является четной функцией переменной ω, т.е. F(-ω)= F(+ω).
Аргумент
(1.35)
Таким образом, спектр непериодической функции характеризуется зависимостью модуля F(ω) и аргумента φ(ω) спектральной плотности.
Отметим связь между значениями спектральной плотности одиночного импульса и амплитудами гармонических составляющих периодической последовательности таких импульсов. Для этого сравним выражение (1.24а) комплексных амплитуд гармонических составляющих периодической последовательности импульсов с периодом Т со спектральной плотностью одиночного импульса той же последовательности (1.29), если импульс существует в промежутке –Т/2 до +Т/2:
. (1.36)