Геометрический смысл задачи линейного программирования

В случае двух переменных модель задачи линейного программирования имеет следующий вид:

(1.8)

Каждое ограничение представляет собой прямую, которая разбивает всё пространство (исходную плоскость) на две полуплоскости, одна из которых удовлетворяет ограничению (рис. 1.1).

Система ограничений представляет выпуклое множество, а в рассматриваемом двухмерном случае - выпуклый многоугольник ограничений (рис.1.2).

В частных случаях многоугольник может обращаться в точку (тогда решение единственно), прямую или отрезок. Если система ограничений противоречива (несовместна), то многоугольник ограничений построить нельзя и задача линейного программирования не имеет решений (рис.1.3).

Многоугольник ограничений может быть не замкнут (рис.1.4). В этом случае целевая функция не ограничена.

В случае n переменных каждое ограничение представляет (n-1)-мерную гиперплоскость, которая делит все пространство на два полупространства. Система ограничений в этом случае дает выпуклый многогранник решений - общую часть n-мерного пространства, удовлетворяющую всем ограничениям.

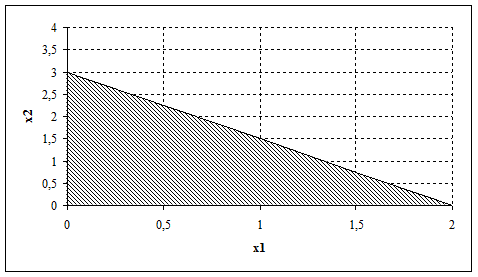
Рис.1.1. Геометрический смысл ограничения

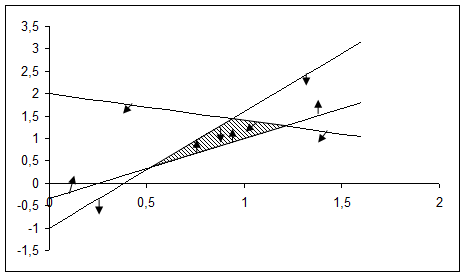
Рис.1.2. Геометрическая интерпретация системы ограничений

Для выяснения геометрического смысла целевой функции придадим переменной Z, различные числовые значения (Z=0, Z=1, Z=2, ..., Z=D).Этим числовым значениям Z соответствует последовательность уравнений и система параллельных прямых в пространстве (рис.1.5).

(1.9)

Рис.1.3. Несовместность системы ограничений

Рис.1.4. Неограниченность целевой функции

Первая прямая (Z=0) проходит через начало координат перпендикулярно (ортогонально) направляющему вектору С=(c₁c₂), последующие прямые параллельны первой и отстоят от нее в направлении вектора С на величину 1, 2, ..., D. В целом переменная Z определяет отклонение точек, лежащих на прямой Z=c₁x₁+c₂x₂ от прямой c₁x₁+c₂x₂=0, проходящей через начало координат. Для того чтобы определить отклонение любой точки от прямой Z=0, достаточно подставить координаты этой точки в уравнение целевой функции.

В n-мерном пространстве целевой функции, приравненной к нулю (Z= c₁x₁+c₂x₂+…+c_jx_j+…+c_nx_n=0), геометрически соответствует (n-1)-мерная гиперплоскость, проходящая через начало координат. Так как линейная форма Z достигает своего экстремального значения в крайней точке (вершине) многогранника ограничений, то геометрически задача линейного программирования заключается в отыскании вершины многогранника допустимых решений, имеющей максимальное уклонение от гиперплоскости, выраженной целевой функцией, приравненной к нулю (рис.1.6).

Рис.1.5.Геометрическая интерпретация целевой функции

Если многогранник ограничений не замкнут (рис.1.4), то уклонение равно бесконечности, так как прямую, параллельную целевой функции, можно перемещать сколько угодно вверх, не выходя за область допустимых значений переменных.

На геометрической интерпретации линейных задач основан графический метод их решения. Этот метод можно эффективно использовать при решении задач с двумя (иногда с тремя) переменными.

Для графического решения задачи линейного программирования необходимо:

1. в принятой системе координат построить уравнения всех ограничений, совокупность которых даст многогранник ограничений;

2. построить уравнение целевой функции, проходящее через начало координат;

3. определить направление роста (убывания) целевой функции, перемещая прямую (плоскость), соответствующую целевой функции, параллельно самой себе или определить градиент целевой функции;

4. в соответствие с целью ЗЛП и направлением роста целевой функции, найти точку касания этой прямой (плоскости) с многоугольником (многогранником) ограничений - вершину многоугольника, имеющую максимальное отклонение от прямой (плоскости), проходящей через начало координат.

Рис.1.6. Геометрический смысл оптимального решения задачи линейного программирования