Математическая логика.
Базовыми понятиями математической логики являются: высказывание, предикат, логические функции (операции), кванторы, логический базис, логические законы (законы алгебры логики).
Под высказыванием в алгебре логики понимается повествовательное предложение (суждение), которое характеризуется определенным значением истинности. В простейших случаях используются два значения истинности: истинно - ложно, да – нет, 1 – 0. Такая алгебра логики, в которой переменная может принимать только два значения истинности, называется бинарной алгеброй логики Буля (по имени ее создателя).
Предикат – выражение, грамматически имеющее форму высказывания, но содержащее переменные некоторых подмножеств, на которых они определены. При замене переменных элементами соответствующего подмножества предикат обращается в высказывание. Частным случаем предиката является пропозиционная функция – функция одной или нескольких переменных, принимающих значения в множестве, состоящем из двух элементов: единица и нуль.
Применение переменных высказываний служит для выражения общности и позволяет формировать законы алгебры логики для любых высказываний данного вида.
Из одного или нескольких высказываний или предикатов можно образовывать новые высказывания или предикаты. Объединение простых высказываний в сложные производится на основе определенных логических правил (операций, функций).
Кроме логических функций, в логике предикатов имеются еще операции, называемые «кванторами».
Кванторы – это специальные операции, которые служат для выражения общности суждений и связанных с ними понятий и позволяют на формальном языке исчисления предикатов говорить не об одном объекте, а о целом классе объектов (это кванторы общности  , существования
, существования 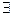 и единственности Е!).
и единственности Е!).
Полную систему логических функций называют логическим базисом. Для того чтобы система функций представляла собой базис, она должна обладать определенными свойствами.
В условиях выполнения требований к базису в алгебре логики доказывают теоремы, демонстрирующие свойства операций над высказываниями. Такие доказуемые теоремы называют законами алгебры логики. Применяя эти законы, формально можно получить правильный результат, не вникая в смысл исследований.
Логические представления сыграли большую роль в развитии теоретической основы алгоритмизации и программирования. В частности, они лежат в основе теории алгоритмов.
Логические представления применяют при исследовании новых структур систем разной природы (технических объектов, текстов и др.), в которых характер взаимодействия между элементами не настолько ясен, чтобы возможно было их представление аналитическими методами, а статистические исследования либо затруднены, либо не привели к выявлению устойчивых закономерностей.
В то же время следует иметь в виду, что с помощью логических алгоритмов можно описать не любые отношения, а лишь те, которые предусмотрены законами алгебры логики.
В настоящее время логические представления широко применяются при исследовании и разработке автоматов разного рода, автоматических систем контроля, при решении задач распознавания образов. На их основе развивается самостоятельный раздел теории формальных языков моделирования проблемных ситуаций и текстов.
В то же время смысловыражающие возможности логических методов ограничены базисом и не всегда позволяют адекватно отобразить реальную проблемную ситуацию. Поэтому стали предприниматься попытки создания логик, в которых переменная может принимать не только крайние значения «истинно» - «ложно», но и какие-либо из промежуточных значений – так называемых многозначных логик, вплоть до непрерывной. Пока эти попытки, в основном, неудачны из-за трудностей создания соответствующего непротиворечивого логического базиса.