Математическое ожидание и дисперсия
Математическим ожиданием дискретной случайной величины называется сумма вида
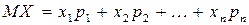
Свойства математического ожидания:
1. M(CX)= СМ(Х); М(С) = С, где С-произвольная постоянная величина.
2.  , если
, если  -
-
взаимно независимые случайные величины.
3.  .
.
Математическое ожидание характеризует среднее значение случайной величины.
Рассеяние случайной величины около среднего значения характеризуют дисперсия и среднее квадратичное отклонение.
Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = М(Х - М(Х))2.
Дисперсию целесообразно вычислять по формуле
D(X) = М(Х2) - (М(Х))2.
Свойства дисперсии:
1. D(CX)= С2D(Х); D(С) = 0, где С-произвольная постоянная величина.
2.  , если
, если  - взаимно независимые случайные величины.
- взаимно независимые случайные величины.
3.  - среднеквадратичное отклонение
- среднеквадратичное отклонение
125. Даны законы распределения двух независимых случайных величин:
| X | ||||
| P | 0,4 | 0,2 | 0,1 | 0,3 |
| Y | |||
| P | 0,5 | 0,2 | 0,3 |
Найти
1) MX, MY
2) DX, DY
3) MZ, DZ, где Z = 2Х + ЗY
126. Задан ряд распределения:
| X | ||||||
| P | 0,4 | 0,2 | 0,2 | 0,05 | 0,1 | 0,05 |
Найти М(Х), D(Х) и М(2Х2 + 3).
127. Даны законы распределения независимых случайньх независимых величин:
| X | -4 | ||
| P | 0,1 | 0,5 | 0,4 |
| Y | ||
| P | 0,5 | 0,5 |
Найти M(Z) и D(Z), если Z = (X + У)/2.
128. В экзаменационном билете три задачи. Вероятность того, что студент правильно решит первую задачу, равна 0,9, вторую – 0,8, третью – 0,7. Пусть X – число правильно решенных задач. Определить числовые характеристики случайной величины: математическое ожидание, дисперсию и среднее квадратическое отклонение.
129. С целью привлечения покупателей компания «Кока-кола» проводит конкурс, согласно которому каждая десятая бутылка напитка, выпущенная фирмой, является призовой. Составить закон распределения числа призовых из четырех приобретенных покупателем бутылок. Найти математическое ожидание и дисперсию этой случайной величины.
130. В партии из 8 деталей 6 деталей – стандартные. Наугад отбираются две детали.Составить закон распределения случайной величины, равной числу стандартных деталей среди отобранных. Найти ее математическое ожидание, дисперсию.
131. Вероятность наличия нужной книги для первой библиотеки равна 0,2; для второй, третьей и четвертой соответственно 0,2, 0,4 и 0,5. Составить закон распределения числа библиотек, которые последовательно посещает студент в поисках нужной книги. Найти математическое ожидание и дисперсию этой случайной величины.
132. Ткачиха обслуживает 3 станка. Вероятности того, что в течение часа станок не потребует внимания, равны соответственно 0,9; 0,8; 0,7. Составить закон распределения для числа станков, потребовавших внимания в течение часа. Найти математическое ожидание и дисперсию этой случайной величины.
133. Молодого человека пригласили на день рождения. Он помнил номер дома, но забыл номер квартиры, помня лишь, что номер однозначный и нечетный. Составить закон распределения числа посещенных квартир для отыскания нужной. Найти математическое ожидание и дисперсию этой случайной величины.
134. Устройство состоит из трех независимо работающих приборов. Вероятности отказа приборов 0,3; 0,64; 0,5.Cоставить закон распределения числа отказавших приборов. Найти математическое ожидание и дисперсию.
135. Фирма имеет 4 грузовых автомобиля. Вероятность выхода на линию каждого автомобиля равна 0,8. Составить закон распределения случайной величины, равной числу автомобилей, которые выйдут на линию в произвольно выбранный день. Найти математическое ожидание и дисперсию этой случайной величины.
136. Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее при первом выстреле равна 0,8, а для каждого последующего выстрела уменьшается на 0,1.Составить закон распределения случайной величины, равной числу попаданий в цель. Найти математическое ожидание и дисперсию этой случайной величины.
137. Вероятность выигрыша по одному билету лотереи равна 0,05. Найти математическое ожидание M(2X-0,5), если случайная величина Xравна числу выигрышных билетов среди 15 купленных.
138. Ветеринар в зоопарке обследует 5 жирафов. Вероятность того, что рост жирафа будет больше 6 метров, равна 0,1. Найти дисперсию D(2X+ 4), если случайная величина Xравна числу обследованных жирафов с ростом более 6 метров.
139. Два консервных завода поставляют продукцию в магазин в пропорции 2:3. Доля продукции высшего качества на первом заводе составляет 90%, а на втором — 80%. В магазине куплено 3 банки консервов. Найти математическое ожидание и среднее квадратичное отклонение числа банок с продукцией высшего качества.
140. Два товароведа проверяют партию изделий. Производительность их труда соотносится как 5:4. Вероятность определения брака первым товароведом составляет 85%, вторым — 90%. Из проверенных изделий отбирают четыре. Найти а) математическое ожидание и б) дисперсию числа годных изделий среди отобранных.
141. В магазин поступили электролампы с трех заводов в пропорции 2:3:5. Доля брака в продукции первого завода — 5%, второго — 2%, третьего — 3%. Покупатель приобрел 3 лампочки. Найти а) математическое ожидание и б) среднее квадратичное отклонение числа качественных лампочек среди купленных.
142. Стороны прямоугольного участка X и У в результате погрешностей измерения оказываются случайными величинами с такими распределениями:
| X | 19,5 | 19,7 | 20,2 | |
| P | 0,2 | 0,05 | 0,7 | 0,05 |
| Y | 29,5 | 29,8 | 30,1 | |
| P | 0,15 | 0,15 | 0,65 | 0,05 |
Найти математическое ожидание площади участка, если известно, что измерения проводились независимыми способами.