Выполнение работы
Задание 1. Определение момента инерции тела динамическим методом.
1. Рассчитать теоретическое значение момента инерции тела относительно центра масс. Так как момент инерции любого тела равен сумме моментов инерции отдельных его элементов, мысленно разделить исследуемое тело на простые элементы, для которых формулы расчета величины момента инерции известны:
а) диск, цилиндр: 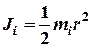 ,
,  – радиус диска, цилиндра (5)*
– радиус диска, цилиндра (5)*
б) пластина: 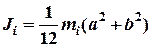 . (6)*
. (6)*
Записать в табл. 1 массы элементов (указаны на элементах). Радиус оси  , радиус диска
, радиус диска 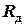 и размеры пластины
и размеры пластины  и
и 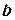 измерить штангенциркулем.
измерить штангенциркулем.
Таблица 1
| № п/п | Элемент тела вращения | Масса, mi, кг | Геометрические параметры, м | Момент инерции 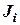 , кг×м2 , кг×м2
|
| Диск | 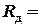
| |||
| Ось (цилиндр) | 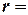
| |||
| Пластина | 
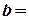
| |||
| Тело | 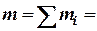
| 
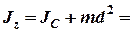
|
Момент инерции тела относительно МОВ определяется теоремой Штейнера
 , (7)*
, (7)*
где 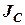 – момент инерции относительно центра масс,
– момент инерции относительно центра масс,  – расстояние от центра масс тела до оси вращения (в этом опыте
– расстояние от центра масс тела до оси вращения (в этом опыте 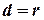 , т.е. радиусу оси).
, т.е. радиусу оси).
Рассчитать момент инерции тела 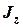 относительно МОВ по формуле (7) и записать в табл. 1.
относительно МОВ по формуле (7) и записать в табл. 1.
2. Записать значение постоянной установки  в табл. 2.
в табл. 2.
3. Проверить правильность положения установки. Для регулировки использовать винты основания. При скатывании тело не должно смещаться к одной из направляющих.
4. Включить секундомер. Установить тело с левой стороны на направляющие на расстоянии 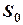 от нижней точки, прижав его к упорам. Положение тела фиксируется магнитом по нажатию кнопки электромагнита.
от нижней точки, прижав его к упорам. Положение тела фиксируется магнитом по нажатию кнопки электромагнита.
5. Нажать кнопку секундомера «Пуск». При этом электромагнит отключится и тело начнет двигаться. Когда тело достигнет нижней точки, секундомер автоматически выключится. Записать время движения тела до нижней точки в табл. 2.
6. Далее, наблюдая за движением тела по инерции, отметить расстояние  , на которое оно поднимется до остановки.
, на которое оно поднимется до остановки.
7. Опыт повторить еще четыре раза при том же расстоянии 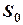 , записывая результаты в табл. 2.
, записывая результаты в табл. 2.
8. Найти средние значения величин 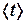 ,
, 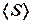 и по формуле (4) рассчитать момент инерции тела
и по формуле (4) рассчитать момент инерции тела 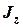 относительно МОВ.
относительно МОВ.
Таблица 2
 рад, рад,  0,51м. 0,51м.
| ||
| № | 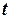 , с , с
|  , м , м
|
| среднее значение | 
| 
|
9. Оценить суммарную относительную погрешность определения момента инерции
 . (8)*
. (8)*
10. Записать окончательный результат с учетом погрешности.
11. Сделать вывод.
Задание 2. Изучение зависимости момента инерции от распределения массы относительно оси вращения.
В этом задании используется тело в виде крестовины, по которой могут перемещаться грузы – цилиндры. Все результаты измерений занести в табл. 3.
1. Определить массу 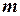 всего тела и радиус
всего тела и радиус  оси тела, и записать постоянную установки
оси тела, и записать постоянную установки  .
.
 2. Установить подвижные цилиндры на минимальном расстоянии
2. Установить подвижные цилиндры на минимальном расстоянии  от оси вращения и измерить это расстояние штангенциркулем.
от оси вращения и измерить это расстояние штангенциркулем.
Примечания:
а) когда грузы находятся на одинаковом расстоянии от оси вращения, тело должно находиться в безразличном положении равновесия на горизонтальных направляющих;
б) так как цилиндры имеют одинаковый размер, расстояние между центрами грузов равно расстоянию между их торцами, которое можно измерить значительно точнее (см. рис. 4);
в) размеры  и
и  могут быть определены с помощью штангенциркуля с минимальной погрешностью, тогда
могут быть определены с помощью штангенциркуля с минимальной погрешностью, тогда
 .
.
Таблица 3
| № |  , м , м
| 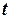 , c , c
|  , м , м
|  , м2 , м2
| 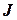 , кг×м2 , кг×м2
|  рад рад
 кг кг
 0,135 кг 0,135 кг
 = м = м
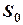 = 0,51 м = 0,51 м
|
3. Установить тело на направляющие на расстоянии 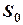 от нижней точки, прижав его к упорам. Положение тела фиксируется магнитом нажатием кнопки электромагнита.
от нижней точки, прижав его к упорам. Положение тела фиксируется магнитом нажатием кнопки электромагнита.
4. Нажать кнопку секундомера «Пуск». При этом электромагнит отключится, и тело начнет двигаться. Когда тело достигнет нижней точки, секундомер автоматически выключится. Записать время движения тела до нижней точки в табл. 3.
5. Отметить расстояние  , на которое пройдет тело, поднимаясь по инерции.
, на которое пройдет тело, поднимаясь по инерции.
6. Повторить измерения п.п. 3–5 при других расстояниях  цилиндров, относительно оси вращения.
цилиндров, относительно оси вращения.
7. Рассчитать  и момент инерции тела
и момент инерции тела 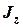 (формула 4) для каждого опыта.
(формула 4) для каждого опыта.
8. Построить график зависимости  (см. рис. 5).
(см. рис. 5).
9. Экстраполируя график  на ось ординат, определить наименьший момент инерции тела
на ось ординат, определить наименьший момент инерции тела  .
.
 10. Выбрать на концах экспериментальной прямой две точки 1 и 2 и рассчитать среднее значение углового коэффициента, т.е. массу грузов.
10. Выбрать на концах экспериментальной прямой две точки 1 и 2 и рассчитать среднее значение углового коэффициента, т.е. массу грузов.
 . (9)*
. (9)*
11. Оценить случайную погрешность определения массы груза как половину случайной погрешности определения углового коэффициента:
 , (10)*
, (10)*
где  – количество экспериментальных точек,
– количество экспериментальных точек,
 – коэффициент Стьюдента.
– коэффициент Стьюдента.
12. Оценить суммарную относительную погрешность, которая характеризует точность выполнения теоремы Штейнера
 . (11)*
. (11)*
13. Сделать выводы.