Корреляционная функция и спектральная плотность мощности стационарного случайной последовательности

 

Случайная последовательность (случайный процесс с дискретным временем) легко может быть определен подобно тому, как выше был определен случайный процесс с непрерывным временем . Также без особых проблем можно ввести понятие стационарности случайных последовательностей в узком и широком смыслах.

Следует отметить, что при обработке случайных сигналов в компьютере либо в цифровом устройстве мы всегда имеем дело именно со случайными последовательностями. Наиболее часто случайные последовательности получают в результате временной дискретизация непрерывного случайного процесса : 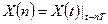, где T – шаг дискретизации. При этом результаты анализа некоторой выборочной реализации случайной последовательности желательности распространить и на свойства процесса .

Для стационарной случайной последовательности корреляционная функция (автокорреляционная последовательность - АКП) определяется следующим образом

. (8)

Здесь - знак математического ожидания, - среднее значение (мат. ожидание) случайной последовательности .

Сравнивая (8) и (4), отмечаем, что . Вопрос о восстановлении корреляционной функции по ее дискретной версии аналогичен вопросу о восстановлении непрерывного сигнала из дискретного сигнала . Ответ: если СПМ процесса финитна (тождественно равна нулю сверх некоторой конечной частоты 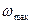), то при достаточно малом шаге дискретизации функция может быть безошибочно восстановлена из 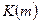при любом .

Теорема Винера-Хинчина для случайных последовательностей определяется следующими двумя выражениями

. (9)

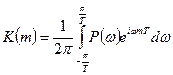. (10)

СПМ периодична по с периодом , поэтому рассматривается на одном периоде либо 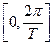. Как она связана с СПМ непрерывного процесса ? Ответ: есть результат наложения всех копий , сдвинутых по частоте на интервалы, кратные . Если выполняется условие , то на интервале .