Решение логических задач с помощью составления логических выражений
Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т.е. записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.
При формализации необходимо учитывать следующее соответствие между логическими операциями и правилами русского языка:
• Отрицание – частица «не»;
• Дизъюнкция – союз «или»;
• Конъюнкция – союзы «и», «а», «но», «хотя», «однако»;
• Эквиваленция – слова «в том и только в том случае», «тогда и только тогда» и другие;
• Импликация – слова «если, то».
Рассмотрим пример. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На аудиториях повесили шутливые таблички. На первой аудитории повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках или обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.
Решение.
Переведем условие на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:
A – «В первой аудитории находится кабинет информатики»;
B – «Во второй аудитории находится кабинет информатики».
Тогда отрицаниям этих высказываний будут соответствовать:
- Высказывание, содержащееся на табличке первой аудитории, соответствует логическому выражению: X=A 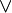 B.
B.
 - «В первой аудитории находится кабинет физики»,
- «В первой аудитории находится кабинет физики»,
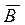 - «Во второй аудитории находится кабинет физики»,
- «Во второй аудитории находится кабинет физики»,
- Высказывание, содержащееся на табличке второй аудитории, соответствует логическому выражению: Y=  .
.
Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные, в соответствии с законом исключенного третьего записываются следующим образом: 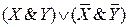 = 1.
= 1.
Подставим вместо X и Y соответствующие формулы:
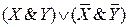 =
= 
Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:  =
=  .
.
В соответствии с законом непротиворечия:  =
=  .
.
Упростим теперь второе слагаемое. В соответствии с законом де Моргана и законом двойного отрицания:  =
=  .
.
В соответствии с законом непротиворечия:  .
.
В результате получаем:  .
.
Полученное логическое выражение оказалось простым и поэтому его можно проанализировать без построения таблицы истинности. Для того чтобы выполнялось равенство  , обе логические переменные должны быть равны 1, а соответствующие им высказывания истинны.
, обе логические переменные должны быть равны 1, а соответствующие им высказывания истинны.
Ответ: В первой аудитории находится кабинет физики, а во второй – кабинет информатики.