Косвенные методы.
а) При измерении растягивающего усилия по относительному удлинению арматуры на ее полной длине или отдельном участке (базе измерительного прибора) используется зависимость между напряжением 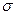 и
и  (закон Гука).
(закон Гука).
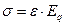 , ,
| (1) |
где 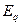 – модуль деформации стали.
– модуль деформации стали.

|
| Рис. 1. |
Этот способ контроля находит широкое применение на производстве, благодаря своей простоте и удовлетворительной точности измерений (± 3-8%). Однако он также может быть использован лишь в процессе натяжения арматуры.
б) Если к натянутому арматурному элементу длины 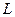 (рис. 1), закрепленному на концах, приложить в середине свободного пролета оттягивающую силу
(рис. 1), закрепленному на концах, приложить в середине свободного пролета оттягивающую силу  , создающую стрелу прогиба
, создающую стрелу прогиба 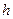 , то величина усилия
, то величина усилия 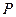 (внутренней силы, действующей вдоль арматуры и растягивающей ее) при
(внутренней силы, действующей вдоль арматуры и растягивающей ее) при 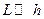 находится из соотношения, которое справедливо для случая, когда жесткостью арматуры можно пренебречь. С увеличением диаметра арматуры точность
находится из соотношения, которое справедливо для случая, когда жесткостью арматуры можно пренебречь. С увеличением диаметра арматуры точность
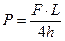
| (2) |
измерений по формуле (2) уменьшается и величина усилия натяжения: может быть приближенно определена по формуле
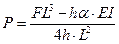 , ,
| (3) |
где 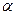 – коэффициент, учитывающий условия закрепления арматуры.
– коэффициент, учитывающий условия закрепления арматуры.
в) В основу данного метода положена зависимость между напряжением 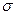 и частотой
и частотой  свободных поперечных колебаний натянутой однородной струны с неподвижно закрепленными концами (рис. 2).
свободных поперечных колебаний натянутой однородной струны с неподвижно закрепленными концами (рис. 2).
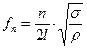 , , 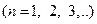 , ,
| (4) |

|
| Рис. 2. Первая (1) и (2) вторая гармоники при шарнирном (а) и (б) жестком закреплении концов напряженной арматуры. |
где  – плотность материала струны;
– плотность материала струны;  – номер гармонии;
– номер гармонии; 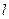 – расстояние между местами закрепления струны.
– расстояние между местами закрепления струны.
Наиболее легко возбудимым при воздействии на арматуру в середине пролета является основной тон колебаний 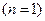 , поэтому все дальнейшие указания по методике контроля напряжений в арматуре относятся именно к нему. Для стального стержня или периодического профиля диаметром
, поэтому все дальнейшие указания по методике контроля напряжений в арматуре относятся именно к нему. Для стального стержня или периодического профиля диаметром  зависимость (4) приобретает вид:
зависимость (4) приобретает вид:
при жестком защемлении концов стержня
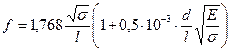 ; ;
| (5) |
при шарнирном креплении концов
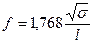 . .
| (6) |
Учет фактического условия закрепления натянутой арматуры в упорах производится введением в формулу (5) безразмерного коэффициента  , значения которого изменяются в пределах от 0 до 1. В общем случае величина напряжения в натянутой арматуре может быть найдена по формуле
, значения которого изменяются в пределах от 0 до 1. В общем случае величина напряжения в натянутой арматуре может быть найдена по формуле
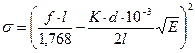 , [кгс/см2] , [кгс/см2]
| (7) |
где  – частота, Гц;
– частота, Гц;
 – диаметр арматуры, мм;
– диаметр арматуры, мм;
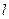 – длина контролируемой арматуры (база измерения), м;
– длина контролируемой арматуры (база измерения), м;
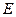 – модуль упругости стали, кгс/см2.
– модуль упругости стали, кгс/см2.
При 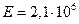 кгс/см2 формулу (7) можно представить в виде
кгс/см2 формулу (7) можно представить в виде
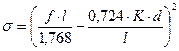 [кгс/см2] [кгс/см2]
| (8) |
Фактическое значение коэффициента  находится путем измерения частот колебаний
находится путем измерения частот колебаний 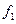 и
и 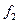 арматуры при одном и том же усилии натяжения на двух базах измерения
арматуры при одном и том же усилии натяжения на двух базах измерения 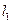 и
и 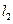 , образованных с помощью специальных подпорок-отсекателей, с последующим расчетом по формуле
, образованных с помощью специальных подпорок-отсекателей, с последующим расчетом по формуле
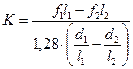 , ,
| (9) |
в которой размерность величин аналогична (7).
   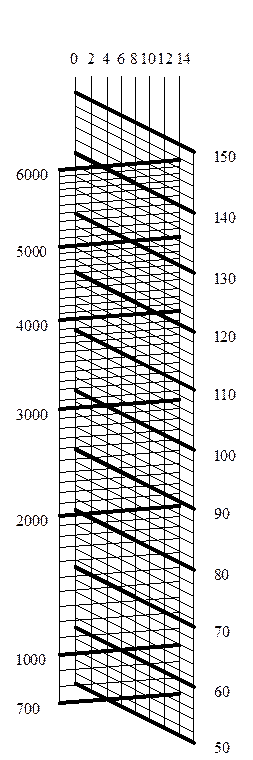
|
| Рис. 3. |
Оценку силы натяжения стержневой арматуры расчетным путем производят относительно редко, гораздо чаще для перехода от измеренной частоты собственных колебаний основного тона к величине механических напряжений используют специальные номограммы (рис. 3).