Входные данные
Известные значения 
– диапазон (столбец), содержащий данные результативного признака выборки.
Известные значения 
– диапазон (столбец), содержащий данные факторов независимого признака выборки.
Константа – 1. Статистика – 1. Нажмите ОК.
6. В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Для раскрытия таблицы данных нажмите F2, затем вместе клавиши «ctrl-shift-enter». Регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
Таблица 2
Значение коэффициента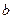 
| Значение коэффициента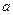 
|
Стандартная ошибка 
| Стандартная ошибка 
|
Индекс детерминации 
| Среднеквадратическое отклонение 
|
| F-статистика | Число степеней свободы |
Регрессионная сумма квадратов
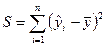
| Остаточная сумма квадратов
|
7. Запишите в бланк отчета значения индекса детерминации и 
. запишите уравнение регрессии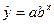 
.
8. Рассчитайте среднюю ошибку аппроксимации.
8.1. Для этого дополните исходную таблицу данных расчетными столбцами:
Таблица 3
| Номер региона |  , руб.
| , руб.
| 
| 
| 
| 
|
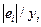
8.2. Рассчитайте последовательно значение результативного признака на основе найденного уравнения регрессии, остатки , модуль остатков , а затем величину .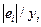
8.3. Используя процедуру Автосумма,вычислите среднее значение 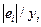. Умножив данное значение на 100%, получите среднюю ошибку аппроксимации.
9. Полученное значение средней ошибки аппроксимации запишите в бланк отчета. Сделайте вывод.
10. С помощью критерия Фишера проведите проверку на статистическую значимость полученного уравнения регрессии на уровне значимости 0,02.
10.1. Найдите табличное значение критерия Фишера. Выделите клетку, в которой должно появиться значение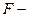 
критерия. В главном меню выберите Вставка/функция. В окне Категория выберите Статистические, затем в окне Функция – FРАСПОБР. Заполните диалоговое окно. Щелкните по кнопке ОК. Появится табличное значение критерия Фишера.
10.2. Из расчетной таблицы 2 найдите наблюдаемое значение критерия Фишера. Сравните критическое значение 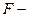критерия с наблюдаемым значением. Сделайте вывод.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. На какие два класса делятся нелинейные уравнения регрессии. Приведите примеры.
2. Каким образом проводится линеаризация уравнения регрессии нелинейного по переменной ?
3. Каким образом проводится линеаризация уравнения регрессии нелинейного по оцениваемым параметрам?
4. Корреляция нелинейной регрессии.
5. Процедура проверки статистической значимости нелинейного уравнения регрессии с помощью критерия Фишера.