Построение переходных процессов в дискретных САУ
Можно изменить время квантования TF, SS, или ZPK-модели sys1, используя команду: sys2 = d2d (sysl, Ts). Новый период квантования Ts не должен быть кратным предыдущему.
Реакцию на единичный скачок для систем с различным периодом квантования можно получить следующим образом:
>> h1=tf([1 0.4], [1 -0.7], 0.1)
Transfer function:
z + 0.4
-------
z - 0.7
Sampling time: 0.1
>> h2=d2d(h1, 0.25)
Transfer function:
z + 1.754
---------
z - 0.41
Sampling time: 0.25
>> step(h1, '-', h2, '-')
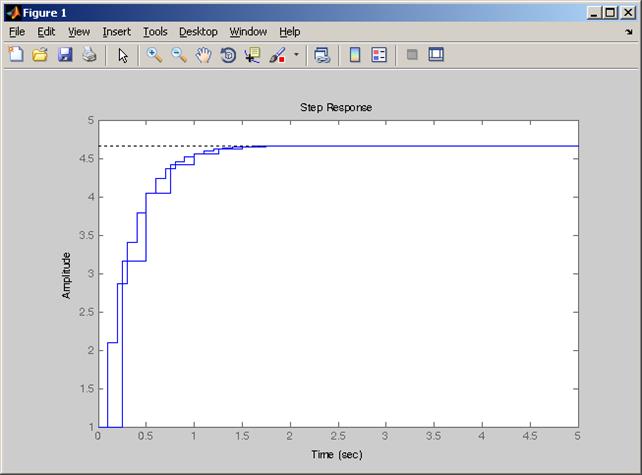
Рисунок 2 – Дискретизация непрерывной модели с экстраполятором нулевого порядка
Можно также использовать c2d для дискретизации систем с запаздыванием:
- задержка tau секунд в непрерывной модели отображена к задержке к тактов в дискретизированной модели, где k = fix(tau/Ts);
- остаточная задержка tau - k*Ts поглощается коэффициентами дискретизированной модели (только для методов с экстраполяцией нулевого и первого порядков).
Например, для того, чтобы дискретизировать передаточную функцию 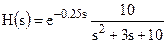 с использованием экстраполяции нулевого порядка при периоде квантования 0,1, следует выполнить:
с использованием экстраполяции нулевого порядка при периоде квантования 0,1, следует выполнить:
>> h=tf(10, [1 3 10], 'inputdelay', 0.25)
Transfer function:
exp(-0.25*s) * ------------------
s^2 + 3 s + 10
>> hd=c2d(h,0.1)
Transfer function:
0.01187 z^2 + 0.06408 z + 0.009721
z^(-3) * -------------------------------------------------
z^2 - 1.655 z + 0.7408
Sampling time: 0.1
Сравнение реакции на ступенчатое воздействие для непрерывной и дискретной систем:
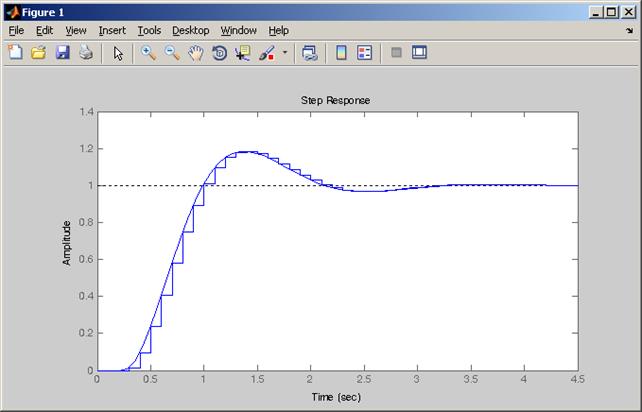
Рисунок 3 – Сравнение реакций на ступенчатое воздействие для непрерывной и дискретной систем
Для построения дискретной модели, заданной в пространстве состояний или в форме передаточной функции системы можно также использовать команду c2dm, записанную одним из следующих способов:
[numDz, denDz] = c2dm (num, den, Ts,'zoh')
[F,G,H,J] = c2dm (А, В, C, D, Ts, 'zoh')
Пример построения дискретной модели по передаточной функции:
Пусть есть непрерывная передаточная функция
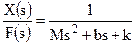 ,
,
где  ;
;  ;
; 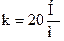 ;
;  ;
; 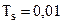 с.
с.
Создадим внутренний файл системы MATLAB, так называемый m-файл. Для этого в главном окне следует выбрать меню File → New → M-File:
M = 1;
b = 10;
k = 20;
num = [1];
den = [M, b, k];
Ts = 1/100;
[numDz, denDz] = c2dm(num, den, Ts, 'zoh')
Далее файл следует сохранить под любым англоязычным именем, например lab1.m. Далее, в меню редактора следует выбрать Debug → Run lab1.m. После этого результат его работы появится в рабочем пространстве MATLAB.
Если теперь в главном окне набрать имя файла, то получим результат его выполнения:
>> lab1
numDz =
1.0e-004 *
0 0.4837 0.4678
denDz =
1.0000 -1.9029 0.9048
Коэффициенты матриц числителя и знаменателя будут представлены по убыванию степеней z. Исходя из вида этих матриц, можно записать передаточную функцию:
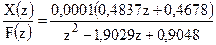
Пример построения дискретной модели по матрицам в пространстве состояний:
Пусть есть непрерывная передаточная функция
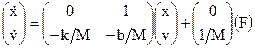

где  ;
;  ;
; 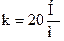 ;
;  ;
; 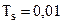 с.
с.
Создаем еще один файл, например, lab1_.m:
M = 1;
b = 10;
k = 20;
A = [0 1; -k/M -b/M];
B = [0; 1/M];
C = [1 0];
D = [0];
Ts = 1/100;
[F, G, H, J] = c2dm(A, B, C, D, Ts, 'zoh')
Запуск этого файла дает следующий результат:
>> lab1_
F =
0.9990 0.0095
-0.1903 0.9039
G =
0.0000
0.0095
H =
1 0
J =
Корни полиномов можно найти, воспользовавшись функцией roots(A).
Последовательность выполнения работы:
1. Для заданной передаточной функции непрерывной САУ (таблица 1) определить передаточные функцию дискретизированной САУ с использованием TF, ZPK и SS – классов, а также обоих видов экстраполяторов (ZOH и FOH).
2. Построить переходные процессы при реакции аналоговой и дискретной САУ на единичное ступенчатое воздействие для случая применения экстраполятора ZOH и FOH, совместив в одной системе координат зависимости для ZOH-системы при периодах квантования  и аналоговой САУ, а в другой – то же для FOH-системы.
и аналоговой САУ, а в другой – то же для FOH-системы.
3. Выполнить пункт 1, используя m-файлы и возможности классов TF и SS.
4. Сделать выводы о влиянии периода квантования на характер переходного процесса.
Таблица 1 – Передаточные функции непрерывной САУ
| Передаточная функция | 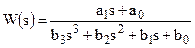
| |||||||
| Вариант | Параметры передаточной функции | |||||||
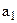
| 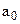
| 
| 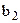
| 
| 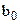
|  , с , с
| ||
| 0,25 | 0,0011 | 0,212 | 0,012 | |||||
| 0,35 | 0,0022 | 0,325 | 0,023 | |||||
| 0,45 | 0,0038 | 0,341 | 0,031 | |||||
| 0,55 | 0,0098 | 0,554 | 0,045 | |||||
| 0,17 | 0,0012 | 0,551 | 0,052 | |||||
| 0,28 | 0,0096 | 0,355 | 0,066 | |||||
| 0,96 | 0,0017 | 0,987 | 0,071 | |||||
| 0,85 | 0,018 | 0,355 | 0,082 | |||||
| 0,37 | 0,036 | 0,478 | 0,093 | |||||
| 0,24 | 0,064 | 0,341 | 0,013 | |||||
| 0,73 | 0,097 | 0,951 | 0,025 | |||||
| 0,032 | 0,581 | 0,036 | ||||||
| 0,95 | 0,0018 | 0,552 | 0,047 | |||||
| 1,2 | 0,0079 | 0,694 | 0,059 | |||||
| 2,5 | 0,0067 | 0,155 | 0,061 | |||||
| 3,7 | 0,0014 | 0,364 | 0,073 | |||||
| 4,6 | 0,0132 | 0,615 | 0,081 | |||||
| 7,3 | 0,0284 | 0,187 | 0,092 | |||||
| 6,2 | 0,0311 | 0,284 | 0,011 | |||||
| 9,2 | 0,154 | 0,384 | 0,023 | |||||
| 4,8 | 0,0715 | 0,145 | 0,038 | |||||
| 7,7 | 0,0641 | 0,525 | 0,042 | |||||
| 6,5 | 0,0321 | 0,441 | 0,058 | |||||
| 0,06 | 0,0212 | 0,454 | 0,063 | |||||
| 0,08 | 0,0025 | 0,547 | 0,071 | |||||
| 0,09 | 0,0052 | 0,581 | 0,086 | |||||
| 0,03 | 0,0038 | 0,945 | 0,091 | |||||
| 12,2 | 0,0087 | 0,874 | 0,017 | |||||
| 13,4 | 0,0141 | 0,664 | 0,024 | |||||
| 16,7 | 0,0251 | 0,554 | 0,039 | |||||
| 11,9 | 0,0541 | 0,158 | 0,041 | |||||
| 8,8 | 0,584 | 0,751 | 0,053 | |||||
| 9,3 | 0,0368 | 0,712 | 0,067 | |||||
| 3,2 | 0,0344 | 0,716 | 0,079 | |||||
| 10,1 | 0,0369 | 0,547 | 0,081 | |||||
| 8,7 | 0,0125 | 0,151 | 0,093 | |||||
| 0,96 | 0,0321 | 0,255 | 0,016 | |||||
| 0,67 | 0,0154 | 0,541 | 0,021 | |||||
| 2,7 | 0,0951 | 0,513 | 0,033 | |||||
| 3,3 | 0,0378 | 0,149 | 0,044 | |||||
| 3,7 | 0,0361 | 0,924 | 0,055 | |||||
| 4,9 | 0,0183 | 0,123 | 0,066 | |||||
| 7,3 | 0,0217 | 0,215 | 0,078 | |||||
Продолжение таблицы 1
| Передаточная функция | 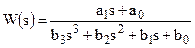
| ||||||
| Вариант | Параметры передаточной функции | ||||||
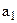
| 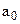
| 
| 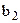
| 
| 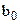
|  , с , с
| |
| 11,8 | 0,0298 | 0,772 | 0,086 | ||||
| 24,9 | 0,0361 | 0,619 | 0,093 | ||||
| 12,5 | 0,0373 | 0,135 | 0,012 | ||||
| 0,8 | 0,0392 | 0,842 | 0,023 | ||||
| 0,61 | 0,0235 | 0,157 | 0,034 | ||||
| 0,92 | 0,0975 | 0,521 | 0,041 | ||||
| 1,35 | 0,0241 | 0,348 | 0,053 | ||||
| 1,96 | 0,0561 | 0,517 | 0,062 | ||||
| 2,37 | 0,0541 | 0,549 | 0,071 |