Г) метод Кьюдера – Ричардсона

Для этого вернемся к нашей матрице в лабораторной работе 1. Мы считали там произведение pj*qj. Доля верных умножить на долю неверных ответов.

Вот такая строчка:

Воспользуемся формулой Кьюдера – Ричардсона:

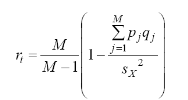
Где М- количество заданий, S в квадрате – дисперсия (мы считали её ранее).

Считаем сумму pj*qj автосуммой. В нашем случае = 1,761. Дисперсия = 5,62.

В итоге получаем r=9/8*(1-1,761/5,62)=0,772.

 

 

2. Вычислить длину теста, если необходимо достигнуть надежности 0,865.

(В качестве исходной надежности взять одну из рассчитанных выше)

Пусть начальная надежность теста равна 0,772 и мы хотим достигнуть надежности 0,865. Во сколько раз надо увеличить длину теста? Для расчетов воспользуемся формулой:

В итоге по формуле получим k= 0,865*(1-0,772)/0,772*(1-0,862)=1,88. Что близко к 2. Получаем, чтобы добиться такой надежности необходимо увеличить тест в 2 раза.

 

3. Определить истинный балл каждого испытуемого, используя регрессионное уравнение

Используя регрессионное уравнение, получим выражение

X с чертой – средний индивидуальный бал. То есть среднее значение по столбику Xi. В нашем случае = 5,8. Коэффициент надежности посчитан ранее, возьмем его равным 0,78.

Создадим небольшую табличку со значениями среднего, коэффициента, баллами (Xi) и из них получим массив Ti.

Затем построим график. По иксам Xi, по игрекам Ti.

Так же можно построить графики для коэффициента корреляции = 0, =0,2 = 1.

Влияние rt на Ti показано ниже:

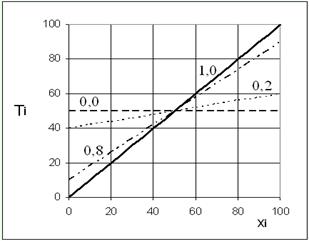
Значения коэффициента надежности показаны возле соответствующих зависимостей.

При rt =1 наблюдаемый Xi и истинный Ti баллы совпадают. Этому случаю соответствует прямая линия, проходящая через начало координат под углом 45 к осям. Если надежность теста равна нулю, то определить истинный балл нельзя, для всех испытуемых получается одно и то же значение, равное среднему баллу. Соответственно, график представляет собой горизонтальную прямую, проходящую на уровне 50 баллов. При других значениях rt получаются промежуточные случаи. На рисунке показаны графики для rt =0,2 и rt =0,8. Все зависимости образованы поворотом прямой линии относительно точки закрепления с координатами (50; 50).

Из приведенных графиков видно, что если наблюдаемый балл испытуемого меньше среднего, то Xi < Ti. Если же наблюдаемый балл больше среднего, то Xi > Ti. Иными словами, наблюдаемый балл у слабых испытуемых меньше, а у сильных - больше истинного индивидуального балла.

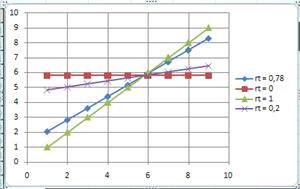
В нашем случае получается вот такие графики, которые мы строим на одной координатной прямой. Для этого правой кнопкой мыши Выбрать Данные. Но до этого нам надо создать несколько клонов нашей таблички и изменить значения rt. И перебить формулы.

4. Найти стандартную ошибку измерения

Где S_X – стандартное отклонение = 2,37259 (корень из дисперсии) был посчитан ранее.

Коэффициент надежности rt – возьмем 0,78122 (по формуле Спирмена-Брауна)

Тогда стандартная ошибка измерения S_E = 2,37*КОРЕНЬ(1-0,78122)=1,10976

5. Построить доверительный интервал для истинного балла каждого испытуемого

Половина доверительного интервала равна δXi = 1,96S_E = 1,96×1,10976 =2,175.

Теперь найдем границы тестового балла, например, для второго испытуемого X2 = 8

(смотрим столбик Xi).

Минимальное значение равно 8-2,175=5,82 ≈ 6. Максимальное равно 8+2,175=10,175 ≈ 10. Следовательно, истинный балл испытуемого №2 находится в промежутке от 6 до 10 баллов. Так для каждого испытуемого (создадим табличку). Просто после рассчетов, в Формате выберев Числовой и уберем знаки после запятой – Excel окргулит значения.