Методика измерения

Выведем рабочую формулу для определения момента инерции тела.

Если предоставить возможность грузу падать, то это падение будет происходить с ускорением , а уравнением поступательного движения груза на нити будет (по второму закону Ньютона (8.19) в проекции на вертикальную ось): , (8.21) где – сила натяжения нити. Отсюда 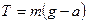. (8.22)

Сила натяжения нити сообщает угловое ускорение вращающемуся маятнику. Момент этой силы относительно оси вращения находим из (8.9); так как нить является касательной к шкиву, плечо силы l совпадает с радиусом шкива r, и тогда: . (8.23)

Тогда уравнение вращательного движения маятника (8.18) запишется в виде , или: . (8.24)

Так как нить нерастяжима и проскальзывания нет, линейное ускорение a груза связано с угловым ускорением шкива соотношением (см. (8.5)):

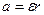. (8.25)

Так как поступательное движение груза m поступательное без начальной скорости, то расстояние (высота ), проходимое грузом за время 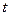, равно 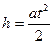, откуда находим ускорение: . (8.26)

Решая совместно (8.24), (8.25) и (8.26), находим момент инерции маятника:

, (8.27) а также выражение для углового ускорения:

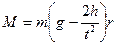(8.28) и момента силы: . (8.29)

 

Упражнение 1

а) Определение углового ускорения маятника Обербека и момента силы натяжения;

б) проверка основного закона динамики вращательного движения:

(при ). (8.30)

1. Измерить штангенциркулем диаметр шкива 3 и найти его радиус .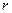

2. Закрепить грузы на концах крестовины в крайних положениях. Добиться равновесия крестовины при любом ее повороте.

3. Положить на тарелочку гирьку массой (около 100 г).

4. Вращая крестовину рукой, намотать нить на шкив.

5. Зафиксировать тарелочку с грузом на высоте h=0.7÷0.8 от наинизшего положения. Записать величину h в таблицу по форме 8.1.

6. Освободить груз и записать в таблицу по форме 8.1 время его опускания.

7. Повторить измерение времени для одной и той же высоты пять раз, рассчитать среднее время и его среднюю погрешность и все результаты записать в таблицу по форме 8.1.

8. Повторить измерения (пункты 4÷6) с массой (150÷200 г), заменив гирьки на тарелочке.

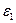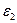9. Рассчитать угловые ускорения и по формуле (8.28), найти их отношение . (8.31)

10. Рассчитать моменты сил и по формуле (8.29), найти их отношение . (8.32)

11. Оценить погрешности определения , и их отношений и .

12. Все результаты занести в таблицы по форме 8.2.

13. Сравнивая и , проверить соотношение , и сделать вывод.

Форма 8.1.

№ m1 = 1,15 кг m2 =0,4 кг h, м Δh r, м Δr
t1, с Δt1i Δt1 t2, с Δt2i Δt2
4,26 0,3 0,2175 6,41 0,238   0,463   0,74 0,005 0,17 0,005
3,97 0,01 6,62 0,028
3,77 0,19 6,75 0,102
3,97 0,01 6,78 0,132
3,83 0,13 6,68 0,032
- t1ср.=3,96 Σ(Δt1i)2= 0,1432 t2ср.= 6,648 Σ(Δt2i)2= 0,06488

 

Форма 8.2.

ε1, с-2 М1, Н.м ε2, с-2 М2, Н.м
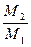
0,5552 1,8975 0,197 0,6641 0,355 0,35
Δε1 ΔМ1 Δε2 ΔМ2
3,359 11,926 1,19 4,25 0,63 3,14

 

Замечание 1: погрешность времени рассчитывается по стандартной методике расчета погрешностей случайной величины:

, (8.38) где коэффициент Стьюдента для числа опытов n=5 и доверительной вероятности α=0.95 равен: tn α=2.57; Δti=|tср.- ti|.

Замечание 2: погрешности ε и М рассчитываются, исходя из формул (33) и (34) соответственно, по стандартной методике расчета погрешностей при косвенных измерениях:

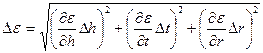, где , , .

 

, где производные равны:

, , , .

Замечание 3: абсолютные погрешности отношений (31) и (32) удобнее считать, предварительно рассчитав относительные погрешности:

; . (8.34)

Упражнение 2.

а) Определение момента инерции маятника Обербека;

б) проверка теоремы Штейнера.

1. Оставив грузы на концах стержней, измерить расстояние R1 от центра тяжести грузов на стержнях до оси вращения.

2. Оставив на тарелочке массу m, повторить 5 раз измерения времени движения груза с другой высотой h (пункты 4÷5 задания 1), рассчитать среднее время, по формуле (8.27) рассчитать момент инерции I1 крестовины с грузами, результаты занести в таблицы по форме 8.3 и 8.4.

3. Передвинуть грузы на середину стержней, измерить расстояние от центра тяжести грузов на стержнях до оси вращения.

4. Повторить измерение времени движения груза m 5 раз, рассчитать среднее время и момент инерции крестовины для нового положения грузиков на стержнях.

5. Повторить измерения и вычисления по пункту 4, передвинув грузики на стержнях вплотную к шкиву, все результаты занести в таблицы по форме 8.3 и 8.4.

 

 

Форма 8.3.

№ h, м m, кг Грузы на концах стержней Грузы посередине стержней Грузы у шкива
t1, с Δt1i Δt1 t2, с Δt2i Δt2 t3, с Δt3i Δt3
0,74 0,4 6,41 0,238 0,463   4,44 0,06 0,103 3,28 0,14 0,165
0,74 0,4 6,62 0,028 4,35 0,03   3,23 0,09
0,74 0,4 6,75 0,102 4,31 0,07 3,22 0,08
0,74 0,4 6,78 0,132 4,3 0,08 2,97 0,17
0,74 0,4 6,68 0,032 4,5 0,12 0,14
  Δh= 0,005   Δm= 0,005   t1ср.= 6,648 Σ(Δt1i)2= 0,06488 t2ср.= 4,38 Σ(Δt2i)2= 0,0302 t3ср.= 3,14 Σ(Δt3i)2= 0,0826

 

Форма 8.4.

I1, кг.м2 I2, кг.м2 I3, кг.м2 R1, м R2, м R3, м
5,65 0,61 0,023 0,22 0,11 0,03 0,002033 0,00266
ΔI1 ΔI2 ΔI3 ΔR1 ΔR2 ΔR3
53,8 11,23 2,15 0,0005 0,0005 0,0005 5,04 5,627

 

6. Оценить погрешность момента инерции .

return false">ссылка скрыта

7. Рассчитать изменение момента инерции маятника Обербека при передвижении грузов с конца стержней на середину по формулам:

, (8.35)

, (8.36)

где m0 = 0.14 кг.

8. Сравнить изменение момента инерции маятника Обербека, рассчитанного с использованием теоремы Штейнера по формулам (8.35) и (8.36) и полученного экспериментально по данным табл. 8.3:

9. Сделать выводы.

Замечание 1: погрешность времени рассчитывается по стандартной методике расчета погрешностей случайной величины по формуле (8.33).

Замечание 2: погрешность I рассчитывается, исходя из формулы (8.27) по стандартной методике расчета погрешностей при косвенных измерениях:

, где производные равны:

; ; ; .
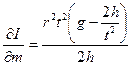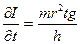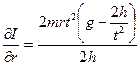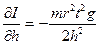