Применение теории размерности. П–теорема
Величины, численное значение которых зависит от принятых масштабов, т. е. от системы единиц измерения, называются размерными. К ним относятся: длина, время, масса, площадь, объём, сила, энергия, момент силы и т. д. Величины, численное значение которых не зависит от применяемой системы единиц измерения, называются безразмерными. Безразмерные величины: углы, отношение двух длин, отношение квадрата длины к площади, отношение энергии к моменту силы и т. п.
Различные физические величины связаны между собой определёнными соотношениями. Поэтому если некоторые из этих величин принять за основные и установить для них какие-то единицы измерения, то единицы измерения всех остальных величин будут определённым образом выражаться через единицы измерения основных величин. Принятые для основных величин единицы измерения называют основными, а все остальные – производными. Обычно в качестве основных принимаются три величины: единица длины – метр [м], единица массы – килограмм [кг] и единица времени – секунда [с]. Размерности всех остальных величин выражаются через основные размерности.
Метод анализа размерностей с использованием неопределённых показателей степеней часто применяется при нахождении зависимостей аэродинамических сил и моментов от основных физических параметров, которые определяют эти силы и моменты.
 Рассмотрим обтекание летательного аппарата потоком воздуха, параллельным оси симметрии со скоростью
Рассмотрим обтекание летательного аппарата потоком воздуха, параллельным оси симметрии со скоростью  .
.
Пусть ЛА (рис. 24) вращается вокруг оси симметрии с угловой скоростью  , которая зависит от времени, и задана производная по времени
, которая зависит от времени, и задана производная по времени  . Требуется получить критерии подобия рассматриваемого течения при определении момента аэродинамических сил вокруг оси
. Требуется получить критерии подобия рассматриваемого течения при определении момента аэродинамических сил вокруг оси  .
.
Будем исходить из теории размерности [10].
Очевидно, что рассматриваемый момент зависит от следующих физических величин: 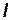 – размах крыла; – размах крыла;  – диаметр корпуса; – диаметр корпуса;  , ,  и и  – плотность, кинематический коэффициент вязкости и давление набегающего потока; – плотность, кинематический коэффициент вязкости и давление набегающего потока;  , ,  , и , и  – были определены ранее; – были определены ранее;  – модуль упругости материала летательного аппарата.
Таким образом, – модуль упругости материала летательного аппарата.
Таким образом,
 . (7.1) . (7.1)
|
Рассмотрим размерности величин, входящих в равенство (7.1):
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Размерности всех приведенных величин представляют собой функции трёх размерных параметров  ,
,  и
и  , отсюда следует, что из всех этих величин имеется не более трёх с независимыми размерностями, а размерности всех остальных величин могут быть выражены через размерности этих трёх. В качестве независимых примем первые три величины, входящие в функцию (7.1):
, отсюда следует, что из всех этих величин имеется не более трёх с независимыми размерностями, а размерности всех остальных величин могут быть выражены через размерности этих трёх. В качестве независимых примем первые три величины, входящие в функцию (7.1):  ,
, 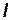 и
и  .
.
Выразим размерности всех остальных параметров через размерности величин  ,
, 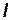 и
и  :
:
 .
.
Приравнивая показатели степени при размерности килограмм, получаем
 .
.
Приравнивая показатели при секунде, найдём
 .
.
Сравнивая показатели при метре, получаем
 ,
,
откуда следует, что
 .
.
Таким образом, можно записать
 . .
| (7.2) |
Для диаметра корпуса 
 . .
| (7.3) |
Для угловой скорости 
 ,
,
откуда получим:
– из размерности  –
–  ;
;
– из размерности  –
–  ;
;
– из размерности  –
–  , т. е.
, т. е.
 . .
| (7.4) |
Для кинематического коэффициента вязкости 
 .
.
Сравнивая размерности, получаем:
– из размерности  –
–  ;
;
– из размерности  –
–  ;
;
– из размерности  –
–  ,
,
поэтому
 . .
| (7.5) |
Для давления невозмущённого потока 
 .
.
Сравнивая размерности, получаем:
– из размерности  –
–  ;
;
– из размерности  –
–  ;
;
– из размерности  –
–  ,
,
поэтому
 . .
| (7.6) |
Для углового ускорения 
 .
.
Сравнивая размерности, получаем:
– из размерности  –
–  ;
;
– из размерности  –
–  ;
;
– из размерности  –
–  ,
,
поэтому
 . .
| (7.7) |
Для модуля упругости 
 . .
| (7.8) |
Соотношение (7.1) не зависит от выбора единиц измерения. Заменим систему единиц измерения так, чтобы параметр  изменился в
изменился в  раз, параметр
раз, параметр 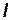 – в
– в  раз и параметр
раз и параметр  – в
– в  раз. Тогда согласно формулам (7.2) – (7.8) остальные величины изменятся таким образом:
раз. Тогда согласно формулам (7.2) – (7.8) остальные величины изменятся таким образом:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
где коэффициенты пропорциональности, входящие в записанные формулы, принимают следующие значения:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Равенство (7.1) в новой системе единиц измерения можно записать так:

  . .
| (7.9) |
Здесь величины  ,
,  и
и  произвольны. Выберем их так, чтобы в соотношении (7.9) уменьшилось количество аргументов функции
произвольны. Выберем их так, чтобы в соотношении (7.9) уменьшилось количество аргументов функции  . Положим
. Положим
 ,
,  и
и  ,
,
тогда
 .
.
В этой формуле все выражения, кроме единиц, есть значения величин в новой системе единиц исчисления и обозначаются через  :
:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 . .
| (7.10) |
Все выражения  имеют нулевую размерность относительно величин
имеют нулевую размерность относительно величин  ,
, 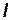 и
и  , значит, они безразмерны. Таким образом,
, значит, они безразмерны. Таким образом,
 . .
| (7.11) |
Формула (7.1) связывает десять размерных величин, а (7.11) – семь безразмерных величин. Количество независимых переменных уменьшилось на число независимых размерностей в формуле (7.1). В этом заключается сущность  –теоремы:
–теоремы:
Если для физического явления существует зависимость между 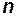 размерными величинами, причём все эти величины выражаются через
размерными величинами, причём все эти величины выражаются через  независимых размерностей, то указанная зависимость может быть преобразована в зависимость между
независимых размерностей, то указанная зависимость может быть преобразована в зависимость между  безразмерными комплексами параметров. Полученные комплексы параметров можно трактовать как критерии подобия рассматриваемого физического явления.
безразмерными комплексами параметров. Полученные комплексы параметров можно трактовать как критерии подобия рассматриваемого физического явления.
Полученные значения параметров  не зависят от выбора первоначальной системы единиц измерения массы, времени и длины. Следовательно, в подобных явлениях эти величины можно рассматривать как безразмерные константы.
не зависят от выбора первоначальной системы единиц измерения массы, времени и длины. Следовательно, в подобных явлениях эти величины можно рассматривать как безразмерные константы.
Проанализируем каждое из равенств (7.10) в отдельности.
Второе равенство (7.10) означает геометрическое подобие обтекаемых тел. Используя параметр  , представляющий собой отношение диаметра корпуса к размаху крыла, записываем
, представляющий собой отношение диаметра корпуса к размаху крыла, записываем
 . .
| (7.12) |
Величина, обратная параметру  из третьего равенства, называется числом Струхаля
из третьего равенства, называется числом Струхаля  :
:
 . .
| (7.13) |
В этом случае равенство (7.13) означает, что в подобных явлениях отношение скорости набегающего потока к окружной скорости вращения для сходственных точек должно быть одинаковым.
Четвёртое из равенств (7.10) даёт число Рейнольдса – критерий подобия по вязкости  :
:
 . .
| (7.14) |
При анализе пятого из равенств (7.10) рассмотрим формулу для скорости звука
 ,
,
т. е.
 .
.
Таким образом, получили число Маха – критерий подобия по сжимаемости

| (7.15) |
и число Пуассона – критерий подобия по теплоёмкостям
 . .
| (7.16) |
Анализируя шестое равенство (7.10), получаем
 . .
| (7.17) |
Возводя в квадрат равенство (7.13), найдём
 . .
| (7.18) |
Перемножив почленно равенства (7.17) и (7.18), запишем
 . .
| (7.19) |
Соотношение (7.19) даёт связь между угловой скоростью и угловым ускорением при вращении с ускорением. Чтобы выяснить физический смысл равенства (7.19), перепишем его в таком виде:
 . .
| (7.20) |
Выражение (7.20) показывает, что в подобных явлениях, осуществляющих вращение с ускорением, отношение касательного ускорения  к нормальному ускорению
к нормальному ускорению  в сходственных точках должно быть одинаковым.
в сходственных точках должно быть одинаковым.
Из первого равенства (7.10) вытекает
 .
.
Умножим почленно это выражение на равенство
 ,
,
тогда
 . .
| (7.21) |
Таким образом, для того, чтобы два рассматриваемых явления были физически подобными, необходимо выполнение равенств (7.12) – (7.20). При этом коэффициенты момента, задаваемые равенством (7.21), будут одинаковы.
В заключение отметим, что в теории размерности и подобия устанавливаются условия, которые должны соблюдаться в опытах с моделями, и выделяются характерные и удобные параметры, определяющие основные эффекты и режимы процессов. Вместе с тем сочетание соображений теории размерности и подобия с общим качественным анализом механизма физических явлений в некоторых случаях является плодотворным теоретическим методом исследования.