Погрешности математического моделирования
Построение любой математической модели и ее реализация связаны с упрощением исходного объекта или явления и внесением погрешностей. Эти погрешности называются погрешностями модели. Погрешность модели является неустранимойпогрешностью. При переходе от математической модели к численному методу возникают погрешности, которые носят название погрешностей метода. Наиболее типичные погрешности метода - это погрешность дискретизациии погрешность усечения (обрыва).При реализации численного метода на ЭВМ возникают погрешности округления.
Остановимся подробней на погрешностях метода и вычислительных погрешностях. В диапазоне пространственно-временных промежутков, в которых функционируют электротехнические устройства, пространство и время можно считать непрерывными субстанциями. Аналитические зависимости электрических величин как функции пространства (линии, площади или объема) и времени обладают этой непрерывностью за исключением точек скачков и разрывов. При этом для любой точки пространства или любого момента времени (в рамках задачи) известно значение данной величины - тока, напряжения, индукции и т. д. Численные же методы дают возможность найти зависимости между величинами дискретно,т.е. в отдельных точках, и непосредственные результаты расчетов могут быть представлены только в табличном виде. Шаг по аргументу, например, времени t, с которым заполняется таблица, называется шагом дискретизации h. Точки аргумента, в которых известны значения функций, называются узлами.Характер же изменения функции между узлами и ее промежуточные значения неизвестны. Чем больше шаг дискретизации, тем выше погрешность численного решения. Точность же решения уравнения при наличии аналитической зависимости от шага не зависит. В основном погрешность дискретизации связана с тем, что для построения численных методов используются приемы, связанные с заменой производных функций конечными разностями [10]. При стремлении шага h к нулю погрешность дискретизации тоже стремится к нулю. Второй погрешностью метода является погрешность усечения (обрыва). Эта погрешность связана с тем, что многие функции, входящие в математическое описание модели, представляются в виде усеченных бесконечных степенных рядов аргумента. Это и дает ошибку усечения (обрыва). Например, sin(x) можно представить в виде степенного ряда
 . (1.6)
. (1.6)
При сохранении двух членов ряда будем иметь усеченную формулу для вычисления синуса: 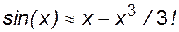 .
.
Погрешность усечения при выводе формул численного интегрирования рассмотрена в главе 4.
Следующим видом погрешности является погрешность округления,связанная с приближенным представлениемвещественных чисел в ЭВМ. Погрешность округления есть вычислительная погрешность.
В отличие от целых чисел, которые в ЭВМ представляются точно, действительные числа представляются в ЭВМ приближенно, с определенной точностью. Это связано со способом представления действительных чисел в ЭВМ. Рассмотрим вопрос более подробно на примере представления действительных чисел в Turbo Pascal 7.0 [2].
Действительные числа в ЭВМ представляются в показательной форме:
 , (1.7)
, (1.7)
где М - мантисса числа; r - основание системы счисления; p - целое число (положительное, отрицательное или нуль) - порядок. Если 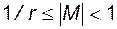 , то число называют нормализованным. Примеры записи нормализованных чисел в показательной форме:
, то число называют нормализованным. Примеры записи нормализованных чисел в показательной форме: 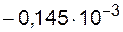 ,
,  и т. д.
и т. д.
Точность числа при таком представлении зависит от количества знаков в мантиссе. Возьмем стандартный тип Паскаля REAL. Под число этого типа в памяти ЭВМ выделяется 6 байт. Один байт равен 8 битам или двоичным разрядам, всего 6х8=48 двоичных разрядов. При этом один разряд отдан под знак числа, 8 - под порядок, 39 - под мантиссу, что соответствует 11 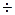 12 значащим десятичным цифрам. Это означает, что числа, отличающиеся в 13-м десятичном знаке, для ЭВМ будут равными. Для многих технических задач данной точности представления чисел бывает недостаточно, и в Турбо Паскале есть тип EXTENDED, который обеспечивает 19
12 значащим десятичным цифрам. Это означает, что числа, отличающиеся в 13-м десятичном знаке, для ЭВМ будут равными. Для многих технических задач данной точности представления чисел бывает недостаточно, и в Турбо Паскале есть тип EXTENDED, который обеспечивает 19  20 десятичных знаков в мантиссе.
20 десятичных знаков в мантиссе.
Как говорилось выше, погрешность дискретизации уменьшается с уменьшением шага дискретизации h. С другой стороны, при расчете величины шага h c его уменьшением приходится вычитать все более близкие числа. Например, если в ЭВМ действительные числа представляются с 5 значащими цифрами, то если 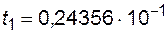 , а
, а 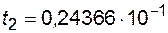 , шаг будет равен h = t2 - t1 =
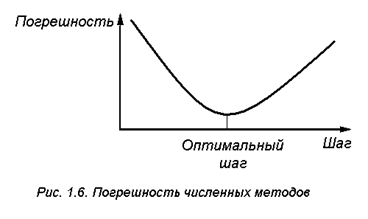
, шаг будет равен h = t2 - t1 =  . Количество значащих цифр сократилось в 5 раз! Следовательно, вычислительные алгоритмы, в которых приходится вычитать близкие по величине числа, могут привести к потере точности решения. В связи с тем, что действия погрешности дискретизации и округления носят противоположный характер, существует оптимальный шаг дискретизации, при котором суммарная погрешность будет минимальна (рис.1.6). Величину оптимального шага можно определить только в условиях конкретной задачи и типа ЭВМ.
. Количество значащих цифр сократилось в 5 раз! Следовательно, вычислительные алгоритмы, в которых приходится вычитать близкие по величине числа, могут привести к потере точности решения. В связи с тем, что действия погрешности дискретизации и округления носят противоположный характер, существует оптимальный шаг дискретизации, при котором суммарная погрешность будет минимальна (рис.1.6). Величину оптимального шага можно определить только в условиях конкретной задачи и типа ЭВМ.
Мы рассмотрели следующие погрешности вычислительного эксперимента:
1) неустранимые - погрешности модели;
2) дискретизации, обрыва (усечения) - погрешности метода;
 |
3) округления - вычислительная погрешность.
Какая из погрешностей преобладает, можно ответить только в конкретном случае. Если объект еще плохо изучен, то погрешности модели будут играть наибольшую роль и т. д. На практике следует стремиться к тому, чтобы все погрешности имели одинаковый порядок.
При математическом моделировании приходится сталкиваться еще с рядом сложных проблем. Главные из них - устойчивостьчисленного метода и плохая обусловленность уравнений, входящих в математическую модель, которые тесно взаимосвязаны. Под устойчивостью численного метода понимают непрерывную зависимость решения от входных данных, равномерную относительно числа уравнений, составляющих дискретную моделью. Непрерывная зависимость от входных данных обозначает, что погрешность результата пропорциональна погрешности входных данных в диапазоне их изменения. Различают устойчивость коэффициентную, разностных схем, по начальным данным и т. д. [6].
Плохо обусловленной (или слабо устойчивой) считается задача, при решении которой погрешности, которые всегда присутствуют в численных методах, приводят к существенно другому результату или к аварийному завершению задачи.
Приведем наглядный пример плохой обусловленности на примере системы из двух линейных уравнений.
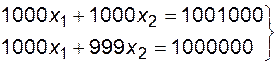 .
.
Её решение будет 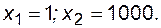 Уменьшим величину коэффициента при х2 во втором уравнении на 0.1% (998 вместо 999). Решение новой системы уравнений дает результат
Уменьшим величину коэффициента при х2 во втором уравнении на 0.1% (998 вместо 999). Решение новой системы уравнений дает результат  Погрешность в коэффициенте в 0.1% привела к погрешности результата более чем в 50000%! Результаты вычислительного эксперимента, проведенного на математической модели, в которой есть уравнения с такими коэффициентами, будут ошибочными.
Погрешность в коэффициенте в 0.1% привела к погрешности результата более чем в 50000%! Результаты вычислительного эксперимента, проведенного на математической модели, в которой есть уравнения с такими коэффициентами, будут ошибочными.
Исходя из сказанного выше, реализующий численные методы вычислительный алгоритм должен бытьустойчивым к накоплению погрешностей и легко реализуемым на ЭВМ.
Вычислительный алгоритм также должен быть еще рационально построен, т.е. должен приводить к результату за минимально возможное число шагов при минимальном использовании памяти ЭВМ. В качестве примера приведем алгоритм вычисления полинома:
return false">ссылка скрыта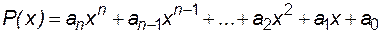 . (1.8)
. (1.8)
по схеме Горнера:
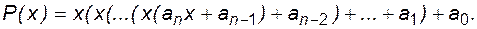 (1.9)
(1.9)