МЕТОДЫ ДОКАЗАТЕЛЬСТВА ТЕОРЕМ
Как мы уже отмечали выше, структура доказательства как логическая конструкция состоит из тезиса, аргументов и демонстрации.
В демонстрации отражается характер логических связей между тезисом и аргументами. В зависимости от вида демонстрации в методической литературе часто употребляются термины «способ доказательства» и «метод доказательства». Покажем, в чем состоит их отличие.
Если доказательство утверждения отличается от другого доказательства того же самого утверждения не логической основой, а последовательностью умозаключений, то будем говорить, что утверждение доказывается двумя различными способами. Если же одно доказательство отличается от другого логической основой, то будем говорить о различных методах доказательства.
Покажем отличие метода от способа доказательства (или решения) на задачах, приведенных ниже.
Задача 1.
На рисунке 2 KM  LN, ∠POM + ∠LOR = 75° и ∠KOR = 58°. Вычислить ∠РОМ и ∠LOP.
LN, ∠POM + ∠LOR = 75° и ∠KOR = 58°. Вычислить ∠РОМ и ∠LOP.
Дано: KM  LN, ∠РОМ + ∠LOR = 75°, ∠KOR = 58°.
LN, ∠РОМ + ∠LOR = 75°, ∠KOR = 58°.
Найти: ∠РОМ и ∠LOP.
Решение
Способ 1
1) ∠ROL = 90° - ∠KOR = 90° - 58° = 32°.
2) ∠РОМ = 75° - ∠ROL = 75° - 32° = 43°.
3) ∠POL = ∠LOM + ∠MOP = 90°+ 43° = 133°.
Способ 2
1) ∠ROL = 90° - 58° = 32°.
2) ∠РОМ = 75° - 32° = 43°.
3) ∠NOP = 90°- 43° = 47°.
4) ∠POL = 180° - ∠NOP = 180°- 43° = 133°.
Способ 3
1) ∠NOР = 360° - 90° - 90° - 58° - 75° = 47°.
2) ∠POL = 180° - ∠NОР = 180° - 47° = 133°.
3) ∠РОМ = 90° - ∠NОР = 90° - 47° = 43°.
Как мы видим, в этих способах решения отличными являются лишь последовательности умозаключений.

Рис.2
Задача 2. Дан квадрат ABCD (рис. 3). Вершина квадрата D соединена с точками М и Р, которые соответственно являются серединами сторон АВ и ВС. Точка М соединена с точкой N, являющейся серединой стороны DC. Докажите, что 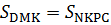 .
.
Способ 1
Из чертежа имеем 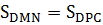 . Отнимем от обеих частей равенства
. Отнимем от обеих частей равенства 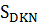 . Получим
. Получим  -
- 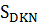 =
=  -
- 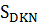 , откуда имеем
, откуда имеем 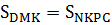 .
.
Способ 2
Из чертежа имеем
 =
=  -
-  -
- 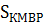 , (1)
, (1)
 =
=  -
-  -
-  . (2)
. (2)
Вычтем из равенства (1) равенство (2). Получим  -
-  =
=  -
-  -
- 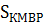 -
-  +
+  +
+ 
Учитывая, что  =
=  , последнее равенство будет иметь вид:
, последнее равенство будет иметь вид:  -
-  =
=  -
-  . Прямоугольник AMND разделен диагональю DM на два равных треугольника: ∆ADM=∆DMN, тогда
. Прямоугольник AMND разделен диагональю DM на два равных треугольника: ∆ADM=∆DMN, тогда  -
-  . Учитывая это, получим
. Учитывая это, получим  -
-  = 0, откуда окончательно имеем
= 0, откуда окончательно имеем  =
=  .
.
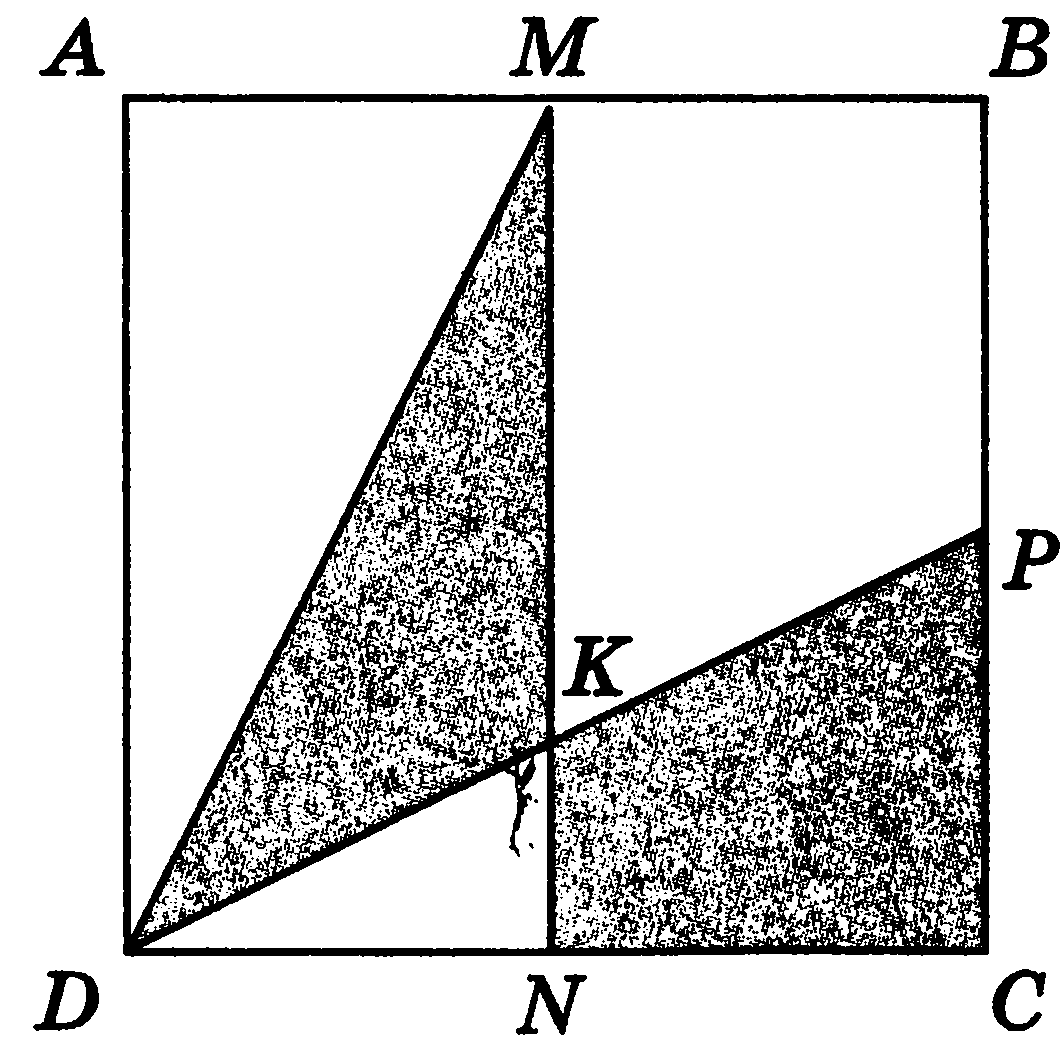
Рис. 3
Задача 3. К плоскости прямоугольника ABCD через точку А проведен перпендикуляр, на котором взята точка К, соединенная с точками В, С и D (рис. 4). Найти АК, если KB = 6 м, КС = 7 м, KD = 5 м.
Решение
Дано: ABCD — прямоугольник; AK ⊥ (АВС)
KB = 6 м,
КС = 7 м,
KD = 5 м.
Найти: АК.
Метод 1
1) Рассмотрим прямоугольный треугольник КDC (∠KDC = 90° по теореме о трех перпендикулярах). По теореме Пифагора имеем DC = 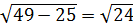 (м).
(м).
2) По свойству прямоугольника имеем AB = DC =  (м).
(м).
3) Из прямоугольного треугольника АВК имеем AK =  (м).
(м).
Метод 2
Введем обозначения: АВ = х, AC = z, AD = y.
1) Из прямоугольного треугольника АКВ  .
.
2) Из прямоугольного треугольника КАС  .
.
3) Из прямоугольного треугольника KAD 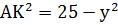 .
.
4) Получим систему уравнений:
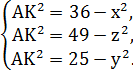
5) Учитывая, что  , система примет вид:
, система примет вид:

Решив систему, получим - 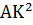 = -12, откуда AK
= -12, откуда AK  (м).
(м).
Мы видим, что в основе этих двух решений лежат совершенно разные логические основы, а значит, речь должна идти о двух разных методах решения: геометрическом и алгебраическом.
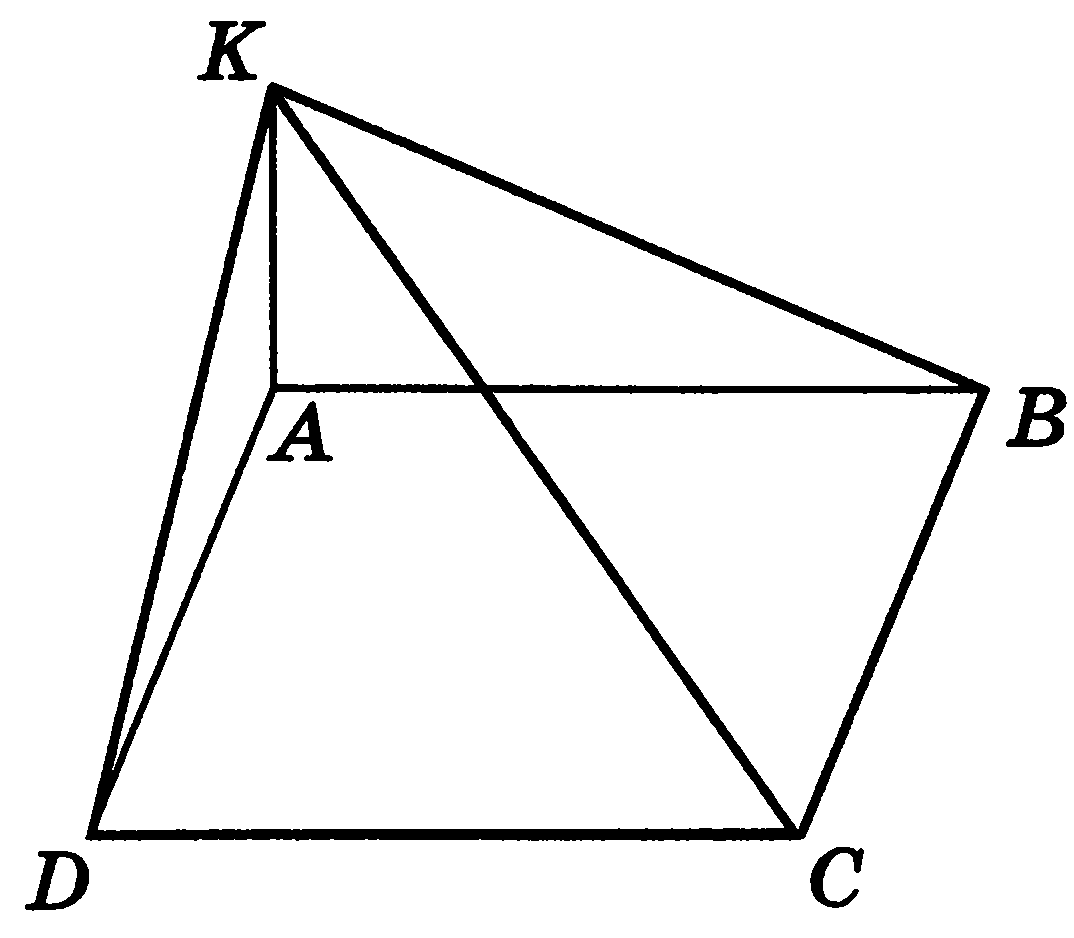
Рис. 4
Задача 4. Доказать, что если в выпуклом четырехугольнике каждая из его диагоналей делит его площадь пополам, то он является параллелограммом.
Метод 1
В четырехугольнике ABCD (рис. 5), в котором АС и BD — диагонали, проведем BN ⊥ AC и DM  АС.
АС.
Рис. 5
По условию  . Учитывая, что
. Учитывая, что 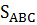 =
= 
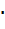 AC
AC  BN, а
BN, а 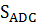 =
=
= 
 AC
AC  DM, имеем
DM, имеем 
 AC
AC  BN =
BN = 
 AC
AC  DM , откуда следует, что BN = DM. ∠MOD = ∠NOB как вертикальные, следовательно, прямоугольные треугольники BON и MOD равны по катету и острому углу, откуда имеем
DM , откуда следует, что BN = DM. ∠MOD = ∠NOB как вертикальные, следовательно, прямоугольные треугольники BON и MOD равны по катету и острому углу, откуда имеем
BO = OD.
Аналогично доказывается равенство OC = OA. Следовательно, мы получили, что в выпуклом четырехугольнике его диагонали в точке пересечения делятся пополам, а это и означает, что четырехугольник – параллелограмм.
Метод 2
Обозначим площадь четырехугольника буквой S. Тогда по условию задачи  и
и 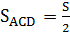 , откуда
, откуда 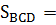
 . И так как площади треугольников BCD и ACD равны и основанием у них является один и тот же отрезок CD, то и высоты этих треугольников будут равными. То есть мы доказали, что все точки отрезка АВ отстоят на одинаковом расстоянии от отрезка CD, а значит, АВ ∥ CD. Аналогично доказывается параллельность отрезков AD и ВС. Из того что в четырехугольнике противоположные стороны оказались попарно параллельны, мы заключаем, что он является параллелограммом.
. И так как площади треугольников BCD и ACD равны и основанием у них является один и тот же отрезок CD, то и высоты этих треугольников будут равными. То есть мы доказали, что все точки отрезка АВ отстоят на одинаковом расстоянии от отрезка CD, а значит, АВ ∥ CD. Аналогично доказывается параллельность отрезков AD и ВС. Из того что в четырехугольнике противоположные стороны оказались попарно параллельны, мы заключаем, что он является параллелограммом.
Метод 3
Построим к предложенной задаче новый чертеж (рис. 6). Проведем через точки В и D прямые 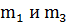 , параллельные АС, через точки А л С — прямые
, параллельные АС, через точки А л С — прямые 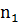 и
и 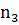 , параллельные BD.
, параллельные BD.

Рис. 6
Так как по условию задачи  и АС — общее основание треугольников AВС и ADC, то высоты этих треугольников равны и прямые
и АС — общее основание треугольников AВС и ADC, то высоты этих треугольников равны и прямые 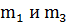 находятся на равных расстояниях от прямой
находятся на равных расстояниях от прямой 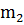 . Аналогично рассуждение о прямых
. Аналогично рассуждение о прямых 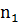 и
и 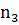 .
.
При центральной симметрии с центром О прямая  переходит в прямую
переходит в прямую 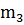 , прямая
, прямая 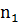 переходит в прямую
переходит в прямую 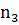 , а прямые
, а прямые 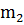 и
и 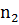 перходят сами в себя как прямые, проходящие через центр симметрии. Тогда эта центральная симметрия переведет точку В в точку D, а точка А в точку С. В силу свойства центральной симметрии AB = CD и BC = DA, а значит, по признаку параллелограмма четырехугольник ABCD — параллелограмм.
перходят сами в себя как прямые, проходящие через центр симметрии. Тогда эта центральная симметрия переведет точку В в точку D, а точка А в точку С. В силу свойства центральной симметрии AB = CD и BC = DA, а значит, по признаку параллелограмма четырехугольник ABCD — параллелограмм.
Доказательство в математике и других дедуктивных науках есть цепочка правильных умозаключений, идущих от исходных для данной теории посылок, признанных истинными, к доказываемому утверждению.
Основным инструментом доказательства теорем являются умозаключения. Умозаключение — рассуждение, в ходе которого из одного или нескольких суждений (называемых посылками умозаключения) выводится новое суждение (называемое заключением или следствием), логически вытекающее из посылок.
Формой дедуктивных умозаключений, используемых при доказательстве теоремы, является силлогизм. В силлогизме содержится три понятия, а состоит он из двух посылок и вывода. Его структуру можно представить в таком виде:
Все М есть Р — большая посылка (БП);
К есть М — меньшая посылка (МП);
К есть Р — вывод (В).
Приведем пример силлогизма: «Все ромбы (М) есть параллелограммы (Р). Квадрат (К) есть ромб (М). Следовательно, квадрат (К) есть параллелограмм (Р)».
Цепочка последовательно связанных силлогизмов, устанавливающая истинность теоремы, называется доказательством теоремы. В качестве примера такой цепочки силлогизмов рассмотрим доказательство теоремы из курса 8 класса: «Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды».
Дано: АВ, CD — хорды, Е — точка пересечения хорд.
Доказать: AE  BE = CE
BE = CE  DE (рис. 7).
DE (рис. 7).

Рис. 7
Доказательство
Силлогизм 1
БП: Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
МП: Вписанные углы (∠1 и ∠2) опираются на одну и ту же дугу BMD.
В: ∠1 = ∠2.
Силлогизм 2
БП: Вертикальные углы равны.
МП: ∠3 и ∠4— вертикальные.
В: ∠3 = ∠4.
Силлогизм 3
БП: Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
МП: Два угла (∠1 = ∠3) треугольника AED соответственно равны двум углам (∠2 = ∠4) треугольника СЕВ.
В: ∆AED  ∆СЕВ.
∆СЕВ.
Силлогизм 4
БП: В подобных треугольниках сходственные стороны пропорциональны.
МП: Стороны АЕ, DE и СЕ, BE — сходственные стороны подобных треугольников AED и СЕВ.
B: 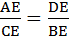 .
.
Силлогизм 5
БП: Произведение крайних членов пропорции равно произведению средних членов пропорции.
МП: АЕ и BE — крайние члены, a DE и СЕ — средние члены одной и той же пропорции.
В: AE  BE = DE
BE = DE  CE.
CE.
Проведение любого доказательства опирается на три блока знаний и умений: содержательный, структурный, логический.
В содержательный блок входят элементы, связанные с ранее изученными математическими понятиями и фактами, которые использованы или в формулировке утверждения, или в качестве аргументов при проведении рассуждений. Эти элементы существенно зависят от логической структуры курса, от его аксиоматики, от методических особенностей изложения и т. д., а поэтому для одной и той же теоремы в различных учебниках содержательный блок может оказаться различным.
В структурный блок входят знания и умения, связанные со структурой утверждения и возможностями ее преобразования. В этот блок входят умения выделять условие и заключение теоремы, преобразовывать логическую форму теоремы с целью получения более простых под теорем и т. д.
Логический блок содержит знания и умения, связанные с правилами логических рассуждений.