Аппроксимация и решение систем линейных уравнений

Краткая теория:

Пусть величина у является функцией аргумента х. На практике часто неизвестна зависимость между х и у или является чрезвычайно сложной, что не позволяет ее использовать. Таким образом, мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра у при любом значении (из некоторой области) параметра х.

Этой цели и служит задача о приближении функций: данную функцию f(x) требуется приближенно заменить некоторой функцией φ(x) так, чтобы отклонение φ(x) от f(x) в заданной области было наименьшим. Функция φ(x) при этом называется аппроксимирующей.

 

Одним из методов поиска аппроксимирующей функции является метод наименьших квадратов:

Для данной функции f(x) требуется построить аппроксимирующую функцию y=j(x, a₀, a₁, …, a_m) , где a₀, a₁, …, a_m – неизвестные постоянные параметры.

Таким образом, требуется среди множества функций найти такую y=j(x, a₀, a₁, …, a_m), при которой отклонение j(x, a₀, a₁, …, a_m) от f(x) принимает минимальное значение. Для этого необходимо найти соответствующие параметры a₀, a₁, …, a_m функции y=j(x, a₀, a₁, …, a_m изсистемы алгебраических уравнений, которая в матричном виде имеет вид:

 

Ф^T(Фa – y) =0или(Ф^ТФ)а=Ф^Тy, где

 

,

 

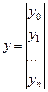
Ф^Т – транспонированная матрица, j(x) = a₀ *j₀ (x)+ a₁*j₁ (x)+ a₂* j₂ (x).

 

Решение систем линейных уравнений (Ф^ТФ)а=Ф^Тy (а – вектор неизвестных параметров) можно осуществить с помощью метода Гаусса или Гаусса-Зейделя.

 

Метод Гаусса:

Для простоты вводятся дополнительные обозначения: С = Ф^ТФ, b=Ф^Тy, т.е исходное уравнение примет вид Ca=b.

Первый этап называется прямым ходом метода и заключается в последовательном исключении неизвестных из уравнений, т.е. в приведении матрицы C к верхнему треугольному виду. На каждом k-ом шаге элементы этой системы уравнений пересчитываются в соответствии с формулами:

 

c_{i j}=c_{i j} -(c_ik /c_kk ) * c_{k j} , i>k , j>k , i=0, 1, …, m, j=0, 1, …, n и

b_i=b_i -(c_ik /c_kk ) * b_k , i>k

Обратный ход метода Гаусса заключается в последовательном определении неизвестных, начиная с n-го.

 

Метод Гаусса-Зейделя:

Требуется найти решение системы линейных уравнений:

 

a₁₁x₁+a₁₂x₂+a₁₃x₃=b₁,

a₂₁x₁+a₂₂x₂+a₂₃x₃=b₂,

a₃₁x₁+a₃₂x₂+a₃₃x₃=b₃,

 

При этом:

 

x₁=(1/a₁₁)*(b₁ - a₁₂x₂ - a₁₃x₃);

x₂=(1/a₂₂)* (b₂ – a₂₁x₁ – a₂₃x₃);

x₃=(1/a₃₃)* (b₃ – a₃₁x₁ – a₃₂x₂).

 

Задаются начальные условия х₁⁽⁰⁾, х₁⁽⁰⁾, х₁⁽⁰⁾. В результате:

x₁⁽¹⁾=(1/a₁₁)* (b₁ - a₁₂x₂⁽⁰⁾ - a₁₃x₃⁽⁰⁾);

x₂⁽¹⁾=(1/a₂₂)* (b₂ – a₂₁x₁⁽¹⁾ – a₂₃x₃⁽⁰⁾);

x₃⁽¹⁾=(1/a₃₃)* (b₃ – a₃₁x₁⁽¹⁾ – a₃₂x₂⁽¹⁾).

Аналогично:

 

x₁^(k)=(1/a₁₁)* (b₁ - a₁₂x₂^(k-1) - a₁₃x₃^(k-1));

x₂^(k)=(1/a₂₂)* (b₂ – a₂₁x₁^(k) – a₂₃x₃^(k-1));

x₃^(k)=(1/a₃₃)* (b₃ – a₃₁x₁^(k) – a₃₂x₂^(k)).

 

Итерационный процесс продолжается до тех пор, пока значения x₁^(k), x₂^(k), x₃^(k) не станут близкими с заданной погрешностью к значениям x₁^(k-1), x₂^(k-1), x₃^(k-1).

Решение задачи:

Построить график аппроксимирующей функции, заданной таблично (см.п.3), используя метод наименьших квадратов (систему линейных уравнений решить методом Гаусса). В качестве формулы для аппроксимации примем:

 

y » j(x) = a₀ *j₀ (x)+ a₁*j₁ (x)+ a₂* j₂ (x) = a₀+a₁*sin(x)+a₂*x

Решение:

Аппроксимирующая функция имеет вид j(x) = a₀+a₁*sin(x)+a₂*x. Требуется найти такие коэффициенты a₀, a₁, a₂, которые бы дали функцию j(x), минимально отклоняющуюся от заданных табличных значений. С помощью метода наименьших квадратов можно получить систему линейных уравнений относительно неизвестных коэффициентов a_i . Матрица Ф имеет вид:

 

 

 

По условию задачи: j₀ (x)=1; j₁ (x)=sin(x); j₂ (x) =x.

 

хi	y
	-4.4
	4.6
	-1.7
	-10

 

 

Справочно: для транспонированной матрицы справедливо следующее:

a_ij=a^T _ji.

 

 

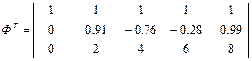
Произведение матриц А размером mxn и B размером nxr есть матрица C размером mxr, где элементы вычисляются следующим образом:

 

, т.е.:

 

;

 

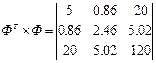Получена система линейных уравнений:

 

 

Требуется найти неизвестные параметры.

Решение осуществляется с помощью метода Гаусса.

 

;

 

 

Прямой ход метода Гаусса. Первый шаг:

;

 

Второй шаг:

;

 

Получена система уравнений:

 

Обратный ход метода Гаусса:

a₂=-24,4/38.92=-0,63

a₁=(-14,95-1,58*(-0,63))/2,32=-6

a₀=(-11,5-20*(-0,63)-0,86*(-6))/5=1,25

Результат: аппроксимирующая функция имеет вид:

y » j(x) = a₀ *j₀ (x)+ a₁*j₁ (x)+ a₂* j₂ (x) =1,25-6*sin(x)-0,63*x

Таблица 3 – Промежуточные значения функции, полученные с помощью аппроксимации методом наименьших квадратов

x	y	x	y	x	y	x	y
0,00	1,25	2,00	-5,47	4,00	3,27	6,00	-0,85
0,20	-0,07	2,20	-4,99	4,20	3,83	6,20	-2,16
0,40	-1,34	2,40	-4,31	4,40	4,19	6,40	-3,48
0,60	-2,52	2,60	-3,48	4,60	4,31	6,60	-4,78
0,80	-3,56	2,80	-2,52	4,80	4,20	6,80	-6,00
1,00	-4,43	3,00	-1,49	5,00	3,85	7,00	-7,10
1,20	-5,10	3,20	-0,42	5,20	3,27	7,20	-8,05
1,40	-5,54	3,40	0,64	5,40	2,48	7,40	-8,80
1,60	-5,76	3,60	1,64	5,60	1,51	7,60	-9,35
1,80	-5,73	3,80	2,53	5,80	0,38	7,80	-9,66
		-9,73

График функции имеет вид, представленный на Рисунке 2.

Рисунок 2 – Аппроксимация методом наименьших квадратов