V.Пример решения задачи оптимального проектирования средствами MS Excel и MathCAD(минимизация стоимости)

Общая постановка задачи

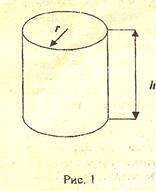
Необходимо выбрать радиус основания r и высоту h цилиндри­ческого открытого резервуара (рис. 1) , обеспечивающих минимальную стоимость материала С=C(r,h) при заданном объ­еме V=V(r,h)=V₀ . Резервуар располагается в помещении с размерами dхdхH ( d- длина и ширина , H - высота помещения). Стоимость 1 м² материала составляет Q у.е.

Математическая постановка задачи

Запишем зависимости:

Площадь поверхности S= 2πrh + πr².

Стоимость С=QS=Q(2πrh + πr²). (1)

Объем V= πr²h. (2)

 

Введем ограничения:

Геометрические(конструктивные):

Радиус основания 0 ≤ r ≤ d/2, (3)

Высота резервуара 0 ≤ h ≤ H. (4)

Функциональные:

Объем V = V₀. (5)

 

Тогда задача математически формулируется следующим образом: найти значения r*, h* , достав­ляющие минимум целевой функции (1):

C* = C(r*, h*) → min

и удовлетворяющие ограничениям (3)-(5).

 

Рассмотрим решение этой задачи с помощью инструмента Поиск решения в среде MS Excel и функции Minimize в среде MathCAD при следующих исход­ных данных:

Q= 10 у .е./ м², V₀=50 м³, d=5 м , Н=7 м.

Решение задачи с помощью инструмента Поиск решения в среде MS Excel