Нелинейные зависимости

 

Как проводить анализ данных, если функция спроса не является линейной? Есть два подхода – параметрический и непараметрический.

В первом случае подбираем подходящее семейство функций и по результатам измерения (опроса) оцениваем параметры. Пример: степенное семейство:

D(p) = cp^{- .}

При этом полезно преобразование переменных, приводящее задачу к линейному виду. В случае степенного семейства необходимо прологарифмировать обе части последнего равенства. Тогда получим:

ln D(p) = ln c + ln p.

Затем обозначим:

у = ln D(p), x = ln p, b =ln c.

Исходя из введенных обозначений, имеем линейное уравнение:

у = x + b.

Задача оценивания параметров степенной зависимости сведена к ранее рассмотренной задаче оценивания параметров линейной функции.

Поясним связь между оценками параметров в этих двух задачах. Будем использовать звездочки для обозначения оценок соответствующих параметров. Допустим, получили выражение:

у^* = - 5x + 3,

тогда, подставляя выражение исходных величин через логарифмы, получим

ln D^*(p) = - 5 ln p + 3.

Далее проводим потенцирование выражения:

e^{ln D (p)} = e^{-5 ln p +3} = e^{-5 ln p} e³ = e³(e^{ln p})^-5 = 20,086p^-5,

т.е.

D^*(p) = 20,086 p^-5.

Аналогично линейному случаю, определим оптимальную розничную цену p_опт. при различных значениях издержек. А именно, решим задачу:

(p – p_0.)D^*(p)

в случае степенной зависимости:

(p – p_0.)с^*p^-α*→ .

Точка, в которой достигается максимум, не меняется при умножении максимизируемой функции на константу. Поэтому переходим к задаче:

(p – p_0.)p^-α* = f(p)→ .

Для нахождения максимума функции продифференцируем ее и приравняем производную к 0:

.

Продифференцируем f(p), используя правило дифференцирования произведения функций:

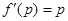^-α* + (p – p₀)( -α^*) p^{-α* -1} =0.

Вынесем общий множитель за скобки:

p^-α*-1[p + (p – p₀))(-α^*)] =0.

Сократим на ненулевой множитель (p^-α*-1):

p + (p – p₀))(-α^*) = 0.

Итак, необходимо решить линейное уравнение относительно неизвестного p:

p – α^*p + p_0.α^* = 0.

Сгруппируем члены с p:

(1 – α^*)p = - p_0.α^*.

Получим оптимальное значение розничной цены:

p_опт. = .

Непараметрический подход применяется тогда, когда подходящее семейство функций подобрать не удается. Тогда используют подходы на основе непараметрических оценок плотности распределения (см. Орлов А.И. Эконометрика. - М.: Экзамен, 2004. -С.145.).