Сравнение методов расчета оптимальной цены

p0	pопт.2	pопт.1
	98,24
	108,24
	118,24
	128,24
	143,24
	153,24

 

Проанализируем результаты, представленные в табл. 2 и 3.

Согласно табл.2, при расчете восстановленной функции D*(p) при p = 200 получаем отрицательную величину (-5,18), что не имеет смысла, т.к. спрос не может быть отрицательным. Рассмотри ситуацию подробнее. Функция спроса убывает, коэффициент a* отрицателен, поэтому рано или поздно прямая уйдет в отрицательную область. Это значит, что приближение функции спроса линейной зависимостью может быть корректно лишь на некотором отрезке, а не на всей прямой. Выясним, при какой цене спрос достигает 0:

D*(p) = (-0,38362)p +71,54 = 0,

p = 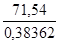= 186,5.

Т.е. корректное приближение функции спроса линейной зависимостью может быть при цене p меньшей, чем 186,5 рублей.

Общепринятых простых методов, позволяющих избежать отрицательных оценок функции спроса, нет. Если получаем отрицательные величины, то должны указать область, в которой линейная зависимость дает корректную оценку, что и сделали выше, когда D*(p) приравняли к 0.

Рассмотрим теперь табл.3. Здесь видим разницу между расчетной оптимальной ценой p_опт.2, полученной с помощью метода наименьших квадратов, и расчетной ценой p_опт.1, найденной исходя только из данных опроса. Это связано с тем, что потребитель всегда склонен к круглым числам (например, большинство назовет 100 руб., а не 102 руб. 27 коп.). Мы же при применении метода наименьших квадратов ищем максимум не только среди названных опрощенными значений, а по более обширному множеству.