Оценивание функции спроса методом наименьших квадратов.

i	Це-на pi	Ni	pi Ni	Спрос D(pi)	D(pi)Ni	Pi2Ni	D(pi)piNi	D*(pi)	Ni[D(pi) – D*(pi)]	Ni[D(pi)-D*(pi)]2
								52,36	-4,718	11,12976
								48,52	-1,0456	0,54664
								42,77	25,852	83,54074
								37,01	3,9432	3,887207
								33,18	12,33	10,13526
								25,51	-45,5392	296,2598
					60				-9,985	19,94005
								6,325	2,0262	1,368495
								2,488	3,0232	4,569869
								-5,18	14,368	103,2197
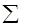
									0,2548	534,5975
		110,8		29,04					SS

Примечание. Здесь n = 50 – число ответов участников опроса.

 

Перейдем к расчету теоретической функции спроса:

D^*(p_i) = a*(p - p_ср.) + b*.

Необходимо найти оценки параметров a* и b*:

a* = =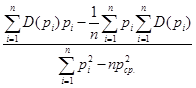

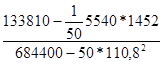= = - 0,38362,

b* = 29,04; d* = b* - a*p_ср.= 29,04 – (- 0,38362)*110,8 = 71,54.

Таким образом, теоретическая функция спроса имеет вид:

D*(p) = (-0,38362)p + 71,54.

Из табл.2 видно, что остаточная сумма квадратов SS = 534,6 (после округления). Исходя из этого, найдем оценку среднего квадратического отклонения:

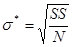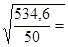= 3,27.

Затем найдем доверительные границы для функции спроса:

D^*(p)_{верхн.\нижн.} = (-0,38362)p + 71,54 1,96 =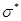

= (-0,38362)p + 71,54 =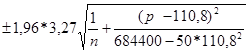

= (-0,38362)p_i +71,54 .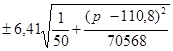

Например, при p = 120

D^*(120) _верхн. = 25,51 + 0,9333 = 26,44,

D^*(120)_нижн. = 25,51 – 0,9333 = 24,57.

Таким образом, при цене 120 руб. товар купят 25-26 человек.

Возьмем теперь другую цену, например 165 руб., тогда

D*(165)_верхн. = (-0,38362)165 +71,54 + 6,41 =

= 8,2427 + 1,5913 = 9,83

D*(165)_нижн. = 8,2427 – 1,5913 = 6,65

Итак, при цене товара 165 руб. его купят от 7 до 10 человек.

Теперь перейдем к расчету оптимальной цены при различных уровнях издержек p₀. Для этого мы должны максимизировать прибыль:

(p - p_0.) D^*(p) = (p_. – p_0.)(a*p + d*).

Продифференцируем это выражение по p и приравняем 0 производную:

,

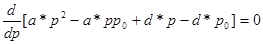2a*p_опт. – а*р₀ +d* = 0,

p_опт. = .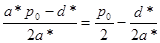

Поскольку a* = -0,38362, a d* = 71,54 ,то

p_опт. = .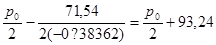

Как видно из последней формулы, при возрастании издержек оптимальная розничная цена также возрастает, но вдвое медленнее.

Сравним (табл.3) оптимальные цены, найденные с помощью метода наименьших квадратов (p_опт.2) и рассчитанные ранее с помощью первого метода (p_опт.1).

 

Таблица 3