ЭКОНОМЕТРИКА
Методические указания к
практическим занятиям
Набережные Челны
Эконометрика. Методические указания к практическим занятиям для студентов специальностей 08011665 – «Математические методы в экономике» и 08080165 – «Прикладная информатика в экономике» / Составитель Розенцвайг А.К. Набережные Челны: Изд-во ИНЭКА, 2006 – 56 с.
Методические указания разработаны на кафедре «Математическое моделирование и информационные технологии в экономике» и предназначены для студентов дневной, заочной и дистанционной формы обучения.
Рецензент: зав.кафедрой математических методов в экономике Набережно-Челнинского филиала КГУ, к.ф.-м.н., доцент Исавнин А.Г.
Печатается по решению научно-методического совета экономического факультета. Камской государственной инженерно-экономической академии
© Камская государственная
инженерно-экономическая
академия, 2006
СОДЕРЖАНИЕ
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1. Особенности построения эконометрической модели . . . . . . 6
1.1. Основные этапы эконометрического исследования . . . 6
1.2. Обоснование формы модельной зависимости . . . . . . . . 8
1.3. Выбор факторов эконометрической модели. . . . . . . . . 12
2. Множественная линейная регрессия. . . . . . . . . . . . . . . . . . . . 17
2.1. Анализ множественной линейной регрессии с помощью метода наименьших квадратов (МНК) . . .. . . . . . . . . . .17
2.2. Теоретические предпосылки применимости МНК . . . 21
2.3. Оценивание коэффициентов множественной линейной регрессии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.4. Интерпретация параметров и уравнения множественной линейной регрессии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3. Анализ качества уравнения регрессии . . . . . . . . . . . . . . . . . . 28
3.1. Характеристики и критерии качества эконометрических
моделей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.2. Дисперсии и стандартные ошибки коэффициентов линейной регрессии . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . 30
3.3. Доверительные интервалы коэффициентов регрессии 32
3.4. Стандартная ошибка и доверительные интервалы уравнения регрессии . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.5. Статистическая значимость уравнения регрессии . . . . 34
4. Стандартизованная форма уравнения множественной линейной регрессии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.1. Стандартизованные переменные . . . . . . . . . . . . . . . . . . 35
4.2. Нормальная система уравнений МНК в стандартизованных переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
4.3. Параметры стандартизованной регрессии . . . . . . . . . . 38
5. Возможности экономического анализа на основе многофакторной регрессионной модели . . . . . . . . . . . . . . . . . . . . . . . 39
5.1. Параметры стандартизованной регрессии . . . . . . . . . . 39
5.2. Средние и частные коэффициенты эластичности . . . . 39
5.3 Коэффициенты линейной корреляции: парные, частные и множественные. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
6. Порядок выполнения и оформления типового примера . . . .45
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
Введение
Постоянно усложняющиеся процессы и явления реальной экономической жизни привели к необходимости создания и совершенствования особых методов их изучения и анализа. При этом широкое распространение получило использование моделирования и количественного анализа. На базе последних выделилось и сформировалось одно из направлений экономических исследований — эконометрика.
Формально «эконометрика» означает «измерения в экономике». Однако область исследований данной дисциплины гораздо шире. Эконометрика — это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели реальных экономических явлений. Обоснование и интерпретация самих моделей является задачей экономической теории, а эконометрика позволяет найти количественное подтверждение либо опровержение того или иного существующего экономического закона либо новой теоретической гипотезы. Одним из важнейших направлений эконометрики является построение прогнозов по различным экономическим показателям.
Эконометрика как научная дисциплина зародилась и получила развитие на основе слияния экономической теории, математической экономики, экономической и математической статистики. Действительно, предмет ее исследования — экономические явления. Но в отличие от экономической теории эконометрика делает упор на количественные, а не на качественные аспекты этих явлений.
Например, экономическая теория утверждает, что спрос на товар с ростом его цены убывает. Но при этом практически неисследованным остается вопрос, как быстро и по какому закону происходит это убывание. Эконометрика отвечает на этот вопрос для каждого конкретного вида товара, места и времени его реализации.
Изучение экономических процессов (взаимосвязей) в эконометрике осуществляется через математические (эконометрические) модели. В этом состоит ее родство с математической экономикой. Но если математическая экономика строит и анализирует обобщенные модели без использования реальных числовых значений, то эконометрика концентрируется на изучении моделей, обоснованных экономической теорией, и сопоставлении их с реальными статистическими данными.
Одной из основных задач экономической статистики является сбор, обработка и представление экономических данных в наглядной форме: в виде таблиц, графиков, диаграмм. Эконометрика также активно пользуется этим инструментарием, но идет дальше, применяя его для анализа теоретически обоснованных экономических взаимосвязей и прогнозирования.
Мощным инструментом эконометрических исследований является аппарат математической статистики. Действительно, большинство экономических показателей носит характер случайных величин, предсказать точные значения которых практически невозможно. Например, весьма сложно предвидеть доход или потребление какого-либо индивидуума, объемы экспорта и импорта страны в течение следующего года и т.д.
Связи между экономическими показателями также не могут носить строгий функциональный характер, а допускают наличие случайных неконтролируемых отклонений (особенно это касается макроэкономических данных). Вследствие этого использование методов математической статистики в эконометрике является естественным и вполне обоснованным. Однако в силу специфики получения статистических данных в экономике (например, в экономике невозможно проведение управляемого эксперимента) эконометрике приходится создавать свои собственные наработки и специальные приемы анализа, которые в математической статистике обычно не рассматривают.
При эконометрическом исследовании имеют место две стороны проблемы обеспечения необходимого качества его результатов – качественная и количественная. Качественная сторона заключается в установлении соответствия между построенной эконометрической моделью и лежащими в ее основе положениями экономической теории. Другая – количественная ‑ состоит в обеспечении наиболее полного соответствия между количественными характеристиками модели и статистической информацией, характерной для поведения изучаемых социально – экономических явлений и процессов в реальных условиях.
1. Особенности построения эконометрических моделей
1.1.Основные этапы эконометрического исследования
Построение эконометрической модели — центральная проблема любого эконометрического исследования, поскольку ее «качество» определяет достоверность и обоснованность результатов анализа тенденций развития, прогнозов рассматриваемых социально-экономических процессов, а также вытекающих из них выводов, в том числе и по вопросам разработки необходимых управленческих мероприятий.
В эконометрических исследованиях обычно предполагается, что закономерности моделируемого процесса складываются под влиянием ряда других явлений, факторов. Обобщенную форму эконометрической модели, описывающей закономерности развития такого процесса, обозначенного переменной у, в зависимости от уровней, воздействующих на него внешних явлений, факторов Xi, i = 1, 2,..., p, можно представить следующим уравнением:
 , (1.1)
, (1.1)
выражающий вид и структуру взаимосвязей между уровнями переменных у, и Xi; e, — случайная ошибка модели, в отношении свойств и характеристик которой, как это будет показано далее, выдвигается ряд дополнительных предположений.
Эконометрика допускает различные предположения относительно «статистического» содержания факторных переменных Xi , в то время как переменная у согласно (1.1) всегда рассматривается как случайная величина. Использование той или иной интерпретации значений переменных эконометрических моделей, как правило, не вносит принципиальные изменения в процедуры их построения, в методы оценки их параметров, но часто сказывается на свойствах полученных результатов.
Выражение (1.1) определяет лишь общий вид эконометрической модели. В конкретных эконометрических исследованиях могут использоваться специальные типы моделей, каждый из которых имеет свои характерные особенности. Эти типы обычно можно классифицировать на основе двух признаков. Во-первых, по виду факторов Xi , во-вторых, по свойствам ошибки модели.
В частности, в моделях регрессии классического типа обычно используются факторы, независимые между собой. Также предполагается, что ошибка модели имеет свойства «белого шума» — случайного процесса с нулевым математическим ожиданием, постоянной конечной дисперсией и нулевой корреляцией между ее разновременными значениями. Это означает, что в ряду ошибки e отсутствуют автокорреляционные связи.
Модели могут различаться и по характеру связей факторов с переменной у. По этому признаку их разделяют на линейные и нелинейные модели. Эконометрические модели могут различаться и по свойствам своих параметров (модели с постоянной и переменной структурой), и по целому ряду других признаков.
Характерная особенность эконометрического исследования заключается в том, что зачастую априорно наиболее подходящий для рассматриваемого процесса тип модели определить не представляется возможным. Но при этом, как правило, на основе содержательного анализа рассматриваемого явления обычно удается выделить приемлемые альтернативные варианты модели и сформировать их исходные предпосылки. По результатам этапов эконометрического исследования эти варианты уточняются, и среди них выбирается тот, который в большей степени соответствует рассматриваемому процессу, явлению.
В общем случае процедуру построения эконометрической модели можно разделить на несколько взаимосвязанных между собой этапов. На каждом из них последовательно решаются задачи, которые имеют следующее содержание:
1. Спецификация модели ‑ анализ специфических свойств рассматриваемых явлений и процессов (предметной области) и обоснование типа моделей, наиболее подходящих для их описания. Отметим, что в общем случае целями этого этапа являются:
1.1. Обоснование формы модели, выражаемой общим математическим уравнением (системой уравнений), связывающим включенные в модель переменные и содержащим неизвестные параметры (коэффициенты).
1.2. Выбор рационального состава включаемых в модель переменных и определение количественных характеристик, отражающих их уровни в прошлые периоды времени (на однородных объектах некоторой совокупности — территориях, предприятиях и т.п.).
2. Параметризация модели ‑ оценка параметров выбранного варианта модели на основании исходных статистических данных, выражающих уровни показателей (переменных) на пространственной совокупности однородных объектов или в различные моменты времени.
3. Верификация модели ‑ проверка качества построенной модели и обоснование вывода о целесообразности ее использования в ходе дальнейшего эконометрического исследования, а также для объяснения поведения изучаемых экономических показателей, прогнозирования и предсказания их поведения.
4. При выводе о нецелесообразности использования построенной эконометрической модели в дальнейших исследованиях следует вернуться к первому (или какому-либо другому этапу) и попытаться выбрать более качественную модификацию модели (другой вариант модели).
Выделенные этапы построения моделей достаточно условны и отражают циклический характер современных экономических исследований: от экономической теории к моделированию; от моделирования к совершенствованию теории и более глубокому пониманию сути происходящих процессов; от понимания сути к осуществлению продуманной и целенаправленной экономической политики. Состав используемых на них процедур, приемов и методов, их очередность зависят от типа разрабатываемой эконометрической модели, особенностей исследуемых экономических процессов, свойств исходных данных и т.п.
1.2. Обоснование формы эконометрической модели
Основные подходы к решению проблем первого этапа исследования в значительной степени базируются на методах содержательного анализа закономерностей рассматриваемых процессов, подкрепляемых по мере необходимости методами общей и математической статистики. Дело в том, что обычно в практических исследованиях функциональный вид эконометрической модели может быть не известным. Часто рассматривают несколько альтернативных их вариантов, среди которых необходимо выбрать наиболее подходящий как с точки зрения требований экономической теории, так и необходимой точности аппроксимации функциональным выражением (1.1) исходного ряда измеренных значений зависимой переменной у.
В этой связи, прежде чем подойти к решению задач первого этапа, необходимо сформировать хотя бы предварительные исходные предпосылки экономического и математического содержания в отношении вида функциональной зависимости. Здесь можно отметить два возможных подхода. В одних случаях составом переменных Xi, i = 1, 2,..., p и формой зависимости (1.1), отражают общепринятую экономическую концепцию. В других ‑ выявляют эмпирические взаимосвязи между ними в ходе конкретных исследований статистических данных.
Примером первого подхода может служить двухфакторная модель Кобба-Дугласа

которую применяют в макроэкономических исследованиях взаимосвязи между объемом полученного валового национального продукта (у) и используемыми производственными ресурсами (Х1 – основные фонды, Х2 – затраты живого труда). Для параметров этой модели известна содержательная экономическая интерпретация, их можно сопоставлять с имеющимися результатами аналогичных исследований.
Второй подход связан с привлечением исходных статистических данных для построения эконометрической модели. В общем случае ими являются известные наборы (массивы) значений зависимой переменной у и независимых факторов Xi. Различают два принципиально различных типа исходных информационных массивов — статический и динамический.
Статический массив представляет собой значения результирующей (зависимой, объясняемой и т.п.) переменной у и влияющих на нее факторов (независимых, объясняющих переменных) Xi, имевших место у объектов однородной совокупности в определенный период времени. Пример таких объектов — однотипные промышленные предприятия (заводы одной отраслевой направленности). В качестве у в практических исследованиях часто рассматривают показатели производительности труда, объемов выпускаемой продукции и некоторые другие. В качестве Xi — влияющие на уровень этих показателей факторы — объемы используемых фондов, численность и квалификация рабочей силы и т.п.
Приведем другой пример статической информации, характерной для социальных исследований. В качестве у часто рассматривают показатели заболеваемости (смертности) населения в регионах страны. Их уровень в каждом из регионов определяют значения независимых факторов, отражающих достигнутый материальный уровень жизни, климатические условия, состояние окружающей среды и т.п. В этом случае необходимая для построения эконометрической модели информация собирается по совокупности регионов страны за определенный фиксированный промежуток времени, например год.
В общем случае будем считать, что необходимая для построения эконометрической модели базового типа (1.1) статическая информация выражается следующими массивами взаимосвязанных (взаимосоответствующих) наборов данных: Такие наборы называют пространственными данными (cross-sectional data) или пространственной выборкой:
 ,
,
где yj — уровень зависимой переменной на j-ом объекте совокупности; xij — уровень i-ro фактора на j-ом объекте статистической совокупности; j = 1, 2, …, n; i = 1, 2, …, p.
Динамическую информацию, которая связывает значения некоторой зависимой переменной у в моменты времени t, называют временным (динамическим) рядом (time-series data).
Исходная информация для построения эконометрических моделей может быть и смешанного типа. Если выборка выражает уровни интересующих нас переменных xit по группе заводов за ряд лет, ее называют панельными данными(panel data).
В случае, когда периодов времени наблюдений Т больше, чем число объектов р, панельные данные называют объединенным временным рядом (pooled time-series). Они связывают значения некоторой зависимой переменной у в моменты времени t со значениями независимых переменных (факторов) xit, рассматриваемых в те же моменты времени, t = l, 2, ..., Т.
В ходе содержательного анализа явление часто рассматривается на качественном уровне, и оперируют достаточно обобщенными понятиями, например, заболеваемость, уровень медицинского обслуживания, качество и уровень жизни, климат, качество рабочей силы и т.п. Часто эконометрическая модель строится именно для выражения закономерности, существующей между явлениями. При построении модели используется исходная информация, наборы показателей, которые уже выражают эти зависимости, их свойства, тенденции в виде количественных характеристик. Следовательно, модельное выражение должно представлять эти реально существующие взаимосвязи.
Для традиционных направлений исследований проблема обоснования состава показателей обычно считается решенной. Например, в макроэкономических исследованиях производительности труда, обычно рассматриваются регламентированные, уже устоявшиеся наборы показателей, значения которых публикуются в статистических сборниках, научных отчетах и других официальных издания Госкомстата. Такие как выработка на одного работающего как показатель, выражающий явление «производительность труда», объемы ВВП ‑ показатель результативности экономики), объемы основных фондов ‑ показатель уровня материальной обеспеченности производственного процесса, экономики) и ряд других.
Вместе с тем в ряде областей эконометрических исследований такие системы показателей не могут быть сформированы столь однозначно. Часто одно и то же явление может быть выражено альтернативными вариантами показателей.
В отсутствие объективных данных в эконометрических исследованиях допускается замена одного показателя другим, косвенно отражающим то же явление. Например, среднедушевой доход как показатель материального уровня жизни может быть заменен среднегодовым товарооборотом на одного жителя региона. Неправильный выбор показателя, представляющего рассматриваемое явление в модели, может существенно повлиять на качество эконометрической модели.
1.3. Выбор факторов эконометрической модели
Проблема обоснования «оптимального» набора факторов обычно решается на основе как содержательного (теоретического), так и количественного (статистического) анализа тенденций рассматриваемых процессов.
На этапе содержательного анализа решается вопрос о целесообразности включения в модель тех или иных факторов, исходя из их экономического смысла. В макроэкономических исследованиях состав факторов, как правило, определяется на основании допущений экономической теории. Пример — двухфакторные производственные функции типа Кобба-Дугласа, которые строятся в предположении, что объем выпуска (производства) экономической системы в основном зависит от размеров используемых основных фондов и количества затраченного труда. Функция типа Кобба-Дугласа учитывает теоретическое предположение о постоянной эластичности выпуска по каждому из производственных факторов.
На этапе содержательного анализа обычно решается проблема установления самого факта наличия взаимосвязей между явлениями. Однако каждое из явлений может быть представлено разными наборами факторами и даже их комбинациями. Поэтому в ряде исследований на основании содержательного анализа однозначно состав независимых переменных модели определить практически невозможно. Могут существовать их альтернативные наборы.
Например, для исследования закономерностей динамики производительности труда на заводе могут быть отобраны следующие факторы: объем основных фондов, энерговооруженность труда, фондовооруженность труда, численность рабочей силы, ее квалификация. При этом квалификация как явление может выражаться разными показателями, например, средним уровнем образования работников, их усредненным квалификационным разрядом и т.п. Кроме того, можно ожидать, что показатели энерговооруженности, фондовооруженности труда, объема основных фондов характеризуют одно и то же явление — уровень материально-технической оснащенности производственного процесса. Таким образом, некоторые из рассматриваемых в таком исследовании показателей, выражающих количественные характеристики независимых переменных, относятся к сходным явлениям.
Факторы, выражающие одну и ту же причину, могут быть тесно взаимосвязаны между собой. Так, уровень розничного товарооборота в основном зависит от среднедушевого дохода; концентрация загрязняющих веществ — от объемов их выбросов. Вследствие этого одновременное включение таких факторов в модель вряд ли целесообразно, поскольку, таким образом, одна и та же причина будет учтена дважды. В результате в общем случае на этапе обоснования эконометрической модели решается задача выбора наиболее предпочтительного состава независимых факторов среди ряда альтернативных вариантов.
Можно выделить два основных подхода к решению этой проблемы. Первый предполагает априорное (до построения модели) исследование характера и силы взаимосвязей между рассматриваемыми переменными, по результатам которого в модель включаются факторы, наиболее значимые по своему «непосредственному» влиянию на зависимую переменную у. И, наоборот, из модели исключаются факторы, которые, либо малозначимы с точки зрения силы своего влияния на эту переменную, либо их сильное влияние на нее обусловлено индуцированными взаимосвязями с другими переменными.
В основе «априорного» подхода лежат следующие предположения.
1. Сильное влияние фактора на зависимую переменную должно подтверждаться определенными количественными характеристиками, важнейшей является их парный линейный коэффициент корреляции, выборочное значение которого рассчитывается на основании имеющейся информации.
Логика использования коэффициента парной корреляции при отборе значимых факторов на практике состоит в следующем. Если значение коэффициента корреляции достаточно велико, т.е. превосходит некоторый эмпирический рубеж (на практике 0,5-0,6), то можно говорить о наличии существенной линейной связи между переменными у и Xi, или о достаточно сильном влиянии Xi на у. Чем больше абсолютное значение ryxi, тем сильнее это влияние (положительное или отрицательное, в зависимости от знака коэффициента парной корреляции).
2. Если два и более факторов выражают одно и то же явление, то, как правило, между ними также должна существовать достаточно сильная взаимосвязь. На это может указать выборочное значение их парного коэффициента корреляции. На практике взаимосвязь между факторами признается существенной, если их коэффициент корреляции достигает величины 0,8-0,9. В таких ситуациях один из этих факторов целесообразно исключить из модели, чтобы одна и та же причина не учитывалась дважды. Однако такое исключение следует проводить только в тех случаях, когда факторы выражают одно и то же явление.
Приведенные рубежные значения (в первом случае — 0,5-0,6; во втором — 0,8-0,9) достаточно условны. В каждом конкретном случае они устанавливаются индивидуально. Значительно усложняет проблему отбора факторов явление ложной корреляции, которое характеризуется достаточно высокими по абсолютной величине значениями коэффициентов парной корреляции с содержательной точки зрения между собой никак не связанных факторов. Иными словами, большие значения парных коэффициентов корреляции могут иметь место и в тех случаях, когда тенденции рассматриваемых процессов совпали случайно, при отсутствии между ними взаимосвязи, обоснованной представлениями соответствующей экономической теории.
Ложная корреляция может помешать при построении «правильной» модели по двум причинам. Во-первых, в модель случайно могут быть введены незначимые с содержательной точки зрения факторы, характеризующиеся значимыми величинами коэффициента парной корреляции. Во-вторых, из модели могут быть исключены значимые с точки зрения влияния на у факторы, в отношении которых ошибочно признана гипотеза о том, что они выражают то же явление, что и другой фактор (факторы), уже включенный в эту модель.
Среди основных причин включения в модель переменных с ложной корреляцией часто называют ненадежность информации, используемой при определении значений факторов в различные моменты времени, трудности формализации факторов, имеющих качественный характер, неустойчивость тенденций изменения рассматриваемых переменных, неправильную форму взаимосвязи между ними и т.п. Основной путь, придерживаясь которого можно избежать ошибок, связанных с понятием «ложной корреляции», связан с проведением качественного анализа проблемы, направленного на обоснование адекватного ей содержания и формы модели.
Второй подход к отбору независимых факторов — можно назвать апостериорным — предполагает первоначально включить в модель все отобранные на этапе содержательного анализа факторы. Уточнение их состава в этом случае производится на основе анализа характеристик качества построенной модели и силы влияния каждого из факторов на зависимую переменную.
Если фактор Xi признается незначимым, его целесообразно удалить из модели. Эта операция приводит к уменьшению общего количества независимых переменных в модели. Таким образом, на практике используют следующую поэтапную процедуру построения окончательного варианта модели на основе апостериорного подхода:
1. В исходный вариант модели включаются все факторы, отобранные в ходе содержательного анализа проблемы. Рассчитывают значения оценок коэффициентов модели, их среднеквадратические ошибки и значения критериев Стьюдента.
2. Из модели удаляют незначимый фактор, характеризующийся наименьшим значением критерия Стьюдента, при условии, что он статистически незначим и формируют новый вариант модели с уменьшенным на один числом факторов.
Заметим, что в модели может быть несколько незначимых факторов. Однако все их одновременно удалять не следует. Возможно, что недостаточная значимость большинства факторов обусловлена влиянием «наихудшего» из незначимых факторов и на следующем шаге расчетов они окажутся значимыми.
3. Процесс отбора факторов считают законченным, когда остающиеся в модели факторы являются значимыми, если полученный вариант модели удовлетворяет и другим критериям ее качества, то процесс построения модели можно считать завершенным в целом.
В противном случае попытаются сформировать другой альтернативный вариант модели, отличающийся от предыдущего либо составом факторов, либо формой их взаимосвязи с зависимой переменной.
Каждый из этих подходов имеет свои преимущества и недостатки. «Априорный» путь отбора факторов не обладает достаточной обоснованностью. Он в большей степени использует «прямые» количественные индикаторы «силы» взаимосвязей между рассматриваемыми величинами и не принимает во внимание в полной мере особенности комплексного влияния независимых факторов на переменную у т.е. своеобразные эффекты «эмерджентности» такого влияния.
Этот эффект выражается в том, что совокупное воздействие нескольких факторов на переменную у, может значительно отличаться от суммы воздействий каждого из них именно в силу наличия внутренних взаимосвязей между независимыми переменными. Вместе с тем использование априорного подхода часто позволяет уточнить некоторые предварительные альтернативные варианты наборов независимых факторов, проверить исходные предпосылки модели относительно правильности выбора формы взаимосвязей между ними.
«Апостериорный» подход к отбору факторов, на первый взгляд, предпочтительнее из-за того, что целесообразность включения в модель каждого из факторов определяется на основании всего комплекса взаимосвязей между переменными. Однако когда общее количество факторов достаточно велико, нет никаких гарантий того, что множество несущественных, а то и ложных взаимосвязей между ними не будет превалировать над основными связями. В результате может оказаться, что в числе первых кандидатов на исключение будут «названы» наиболее важные, значимые с точки зрения влияния на переменную у, факторы. Поэтому в сложных случаях, т.е. при наличии большого числа отобранных для включения в модель на этапе содержательного анализа факторов, полезно сочетать при обосновании их «оптимального» состава оба подхода, как априорный, так и апостериорный.
2. Множественная линейная регрессия
Множественный регрессионный анализ является расширением парного регрессионного анализа. О применяется в тех случаям, когда поведение объясняемой, зависимой переменной необходимо связать с влиянием более чем одной факторной, независимой переменной. Хотя определенная часть многофакторного анализа представляет собой непосредственное обобщение понятий парной регрессионной модели, при выполнении его может возникнуть ряд принципиально новых задач.
Так, при оценке влияния каждой независимой переменной необходимо уметь разграничивать ее воздействие на объясняемую переменную от воздействия других независимых переменных. При этом множественный корреляционный анализ сводится к анализу парных, частных корреляций. На практике обычно ограничиваются определением их обобщенных числовых характеристик, таких как частные коэффициенты эластичности, частные коэффициенты корреляции, стандартизованные коэффициенты множественной регрессии.
Затем решаются задачи спецификации регрессионной модели, одна из которых состоит в определении объема и состава совокупности независимых переменных, которые могут оказывать влияние на объясняемую переменную. Хотя это часто делается из априорных соображений или на основании соответствующей экономической (качественной) теории, некоторые переменные могут в силу индивидуальных особенностей изучаемых объектов не подходить для модели. В качестве наиболее характерных из них можно назвать мультиколлинеарность или автокоррелированность факторных переменных.
2.1. Анализ множественной линейной регрессии с помощью
метода наименьших квадратов (МНК)
В данном разделе полагается, что рассматривается модель регрессии, которая специфицирована правильно. Обратное, если исходные предположения оказались неверными, можно установить только на основании качества полученной модели. Следовательно, этот этап является исходным для проведения множественного регрессионного анализа даже в самом сложном случае, поскольку только он, а точнее его результаты могут дать основания для дальнейшего уточнения модельных представлений. В таком случае выполняются необходимые изменения и дополнения в спецификации модели, и анализ повторяется после уточнения модели до тех пор, пока не будут получены удовлетворительные результаты.
На любой экономический показатель в реальных условиях обычно оказывает влияние не один, а несколько и не всегда независимых факторов. Например, спрос на некоторый вид товара определяется не только ценой данного товара, но и ценами на замещающие и дополняющие товары, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии M(Y/Х = х) = f(x) рассматривается множественная регрессия
M(Y/Х1 = х1, Х2 = х2, …, Хр = Хр) = f(x1, х2, …, хр) (2.1)
Задача оценки статистической взаимосвязи переменных Y и Х1, Х2, ..., ХР формулируется аналогично случаю парной регрессии. Уравнение множественной регрессии может быть представлено в виде
Y = f( B, X) + e (2.2)
где X — вектор независимых (объясняющих) переменных; В — вектор параметров уравнения (подлежащих определению); e - случайная ошибка (отклонение); Y — зависимая (объясняемая) переменная.
Предполагается, что для данной генеральной совокупности именно функция f связывает исследуемую переменную Y с вектором независимых переменных X.
Рассмотрим самую употребляемую и наиболее простую для статистического анализа и экономической интерпретации модель множественной линейной регрессии. Для этого имеются, по крайней мере, две существенные причины.
Во-первых, уравнение регрессии является линейным, если система случайных величин (X1, X2, ..., ХР, Y) имеет совместный нормальный закон распределения. Предположение о нормальном распределении может быть в ряде случаев обосновано с помощью предельных теорем теории вероятностей. Часто такое предположение принимается в качестве гипотезы, когда при последующем анализе и интерпретации его результатов не возникает явных противоречий.
Вторая причина, по которой линейная регрессионная модель предпочтительней других, состоит в том, что при использовании ее для прогноза риск значительной ошибки оказывается минимальным.
Теоретическое линейное уравнение регрессии имеет вид:
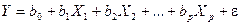 , (2.3)
, (2.3)
или для индивидуальных наблюдений с номером i:
 (2.4)
(2.4)
где i = 1, 2, ..., п.
Здесь В = (b0, b1, ,bР) — вектор размерности (р+1) неизвестных параметров bj, j = 0, 1, 2, ..., р, называется j-ым теоретическим коэффициентом регрессии (частичным коэффициентом регрессии). Он характеризует чувствительность величины Y к изменению Xj. Другими словами, он отражает влияние на условное математическое ожидание M(Y/Х1 = х1, Х2 = х2, …, Хр = xр) зависимой переменной Y объясняющей переменной Хj при условии, что все другие объясняющие переменные модели остаются постоянными. b0 — свободный член, определяющий значение Y в случае, когда все объясняющие переменные Xj равны нулю.
После выбора линейной функции в качестве модели зависимости необходимо оценить параметры регрессии.
Пусть имеется n наблюдений вектора объясняющих переменных X = (1, X1, X2, ..., ХР) и зависимой переменной Y:
(1, хi1, xi2, …, xip, yi), i = 1, 2, …, n.
Для того чтобы однозначно можно было бы решить задачу отыскания параметров b0, b1, … , bР (т.е. найти некоторый наилучший вектор В), должно выполняться неравенство n > p + 1. Если это неравенство не будет выполняться, то существует бесконечно много различных векторов параметров, при которых линейная формула связи между X и Yбудет абсолютно точно соответствовать имеющимся наблюдениям. При этом, если n = p + 1, то оценки коэффициентов вектора В рассчитываются единственным образом — путем решения системы p + 1 линейного уравнения:
 (2.5)
(2.5)
где i = 1, 2, ..., п.
Например, для однозначного определения оценок параметров уравнения регрессии Y = bо + b1 X1 + b2 X2 достаточно иметь выборку из трех наблюдений (1, хi1, хi2, yi), i = 1, 2, 3. В этом случае найденные значения параметров b0, b1, b2 определяют такую плоскость Y = bо + b1 X1 + b2 X2 в трехмерном пространстве, которая пройдет именно через имеющиеся три точки.
С другой стороны, добавление в выборку к имеющимся трем наблюдениям еще одного приведет к тому, что четвертая точка (х41, х42, х43, y4) практически всегда будет лежать вне построенной плоскости (и, возможно, достаточно далеко). Это потребует определенной переоценки параметров.
Таким образом, вполне логичен следующий вывод: если число наблюдений больше минимально необходимой величины, т.е. n > p + 1, то уже нельзя подобрать линейную форму, в точности удовлетворяющую всем наблюдениям. Поэтому возникает необходимость оптимизации, т.е. оценивания параметров b0, b1, …, bР, при которых формула регрессии дает наилучшее приближение одновременно для всех имеющихся наблюдений.
В данном случае число n = n - p - 1 называется числом степеней свободы. Нетрудно заметить, что если число степеней свободы невелико, то статистическая надежность оцениваемой формулы невысока. Например, вероятность надежного вывода (получения наиболее реалистичных оценок) по трем наблюдениям существенно ниже, чем по тридцати. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений превосходило число оцениваемых параметров, по крайней мере, в 3 раза.
Прежде чем перейти к описанию алгоритма нахождения оценок коэффициентов регрессии, отметим желательность выполнимости ряда предпосылок МНК, которые позволят обосновать характерные особенности регрессионного анализа в рамках классической линейной многофакторной модели.
2.2. Теоретические предпосылки МНК
1°. Математическое ожидание случайного отклонения ei равно нулю для всех наблюдений:

2°. Наличие гомоскедастичности (постоянство дисперсии случайных отклонений). Дисперсия случайных отклонений ei должна быть постоянной:
D(ei) = D(ej) = s2 для любых наблюдений с номером i и j.
3°. Отсутствие автокорреляции. Случайные отклонения ei и ej не должны зависеть друг от друга для всех i  j.
j.

4°. Случайное отклонение должно быть независимым от объясняющих переменных:
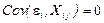 .
.
5°. Модель эмпирической регрессии должна являться линейной относительно параметров. Это ограничение не распространяется на факторные переменные.
6°. Отсутствие мультиколлинеарности. Между объясняющими переменными должна отсутствовать строгая (сильная) линейная зависимость.
7°. Случайные величины ‑ошибки ei, i = 1, 2, ..., п, должны иметь нормальный закон распределения (ei ~ N(0, se )).
Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.
Как и в случае парной регрессии, истинные значения параметров bj с помощью случайной выборки получить невозможно. В этом случае вместо теоретического уравнения регрессии (2.3) оценивается так называемое эмпирическое уравнение регрессии. Эмпирическое уравнение регрессии представим в виде:
 (2.6)
(2.6)
Здесь  — оценки теоретических значений b0, b1, ...,bp коэффициентов регрессии (эмпирические коэффициенты регрессий); е — эмпирическая оценка неизвестного случайного отклонения e. Для индивидуальных наблюдений имеем:
— оценки теоретических значений b0, b1, ...,bp коэффициентов регрессии (эмпирические коэффициенты регрессий); е — эмпирическая оценка неизвестного случайного отклонения e. Для индивидуальных наблюдений имеем:
 (2.7)
(2.7)
Оцененное уравнение в первую очередь должно описывать общую закономерную тенденцию изменения зависимой переменной Y. При этом необходимо иметь возможность оценить случайные отклонения измеренных значений yi от таких неслучайных расчетных значений.
По данным выборки объема п: (1, хi1, xi2, ..., xip, yi), i = 1, 2, ..., п, требуется оценить значения параметров bj вектора B , т.е. провести параметризацию выбранной модели (здесь хij, j = 0, 1, 2, ..., p значение переменной Xj в i-oм наблюдении).
При выполнении перечисленных выше предпосылок МНК относительно ошибок ei оценки  коэффициентов b0, b1, ..., bp множественной линейной регрессии с помощью МНК являются несмещенными, эффективными и состоятельными (т.е. BLUE-оценками).
коэффициентов b0, b1, ..., bp множественной линейной регрессии с помощью МНК являются несмещенными, эффективными и состоятельными (т.е. BLUE-оценками).
На основании (5.7) отклонение ei значения зависимой переменной Y от модельного значения  , соответствующего уравнению регрессии в i-oм наблюдении (i = 1, 2, ..., n), рассчитывается по формуле:
, соответствующего уравнению регрессии в i-oм наблюдении (i = 1, 2, ..., n), рассчитывается по формуле:
 (2.8)
(2.8)
Наиболее распространенным методом оценки параметров уравнения множественной линейной регрессии является метод наименьших квадратов (МНК). Его суть состоит в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной Y от ее расчетных значений  , получаемых с помощью модельного уравнения регрессии:
, получаемых с помощью модельного уравнения регрессии:

По МНК для нахождения оценок минимизируется следующая функция, квадратичная относительно коэффициентов регрессии b0, b1, ..., bp:
 . (2.9)
. (2.9)
Данная функция является квадратичной относительно неизвестных величин bj, j = 0, 1, ..., p. Она ограничена снизу, следовательно, имеет минимум. Необходимым условием минимума функции S(b0, b1, ..., bp) является равенство нулю всех ее частных производных по bj. Частные производные квадратичной функции (2.9) являются линейными функциям относительно искомых оценок коэффициентов регрессии:
 ,
,
 , (2.10)
, (2.10)
где j = 1, 2, ..., p.
Приравнивая их к нулю, получаем нормальную систему р + 1 линейных уравнений с р + 1 неизвестными оценками коэффициентов регрессии, что является одним из достоинств метода МНК. Такая система имеет обычно единственное решение:
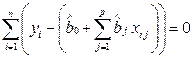 ,
,

 , (2.11)
, (2.11)
где j = 1, 2, ..., p.
В исключительных случаях, когда столбцы системы линейных уравнений линейно зависимы, она имеет бесконечно много решений или не имеет решения вовсе. Однако данные реальных статистических наблюдений к таким исключительным случаям практически никогда не приводят.
Система линейных уравнений относительно неизвестных оценок параметров линейной модели имеет следующий вид:
 После деления всех уравнений системы на объем выборки n все суммарные величины преобразуются в соответствующие средние величины:
После деления всех уравнений системы на объем выборки n все суммарные величины преобразуются в соответствующие средние величины:
 (2.12)
(2.12)
Из первого уравнения можно определить величину коэффициента регрессии  :
:

Подставляя его в уравнение (2.8), получим следующую форму записи эмпирического линейного уравнения множественной регрессии:

Нормальную систему линейных уравнений МНК (2.11) наиболее наглядно можно представить с помощью векторно-матричной формы записи.
2.3. Оценивание коэффициентов множественной
линейной регрессии
Представим данные наблюдений и соответствующие коэффициенты в матричной форме.

Здесь Y — n - мерный вектор-столбец наблюдений зависимой переменной Y; X — матрица размерности п х (p + 1), в которой i - я строка (i = 1, 2, ... , п) представляет наблюдение вектора значений независимых переменных X1, X2, ..., ХР; единица соответствует переменной при свободном члене bo, В — вектор-столбец размерности (p+1) параметров уравнения регрессии (2.8); е — вектор-столбец отклонений выборочных (реальных) значений yi зависимой переменной Y (2.7) от значений  , размерности п,получаемых из модельного уравнения регрессии:
, размерности п,получаемых из модельного уравнения регрессии:
 (2.14)
(2.14)
Сумма квадратов отклонений МНК в матричном виде запишется следующим образом:
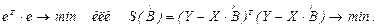
Условие экстремума:  . (2.15)
. (2.15)
Частные производные по параметрам в матричной форме вычисляются следующим образом:

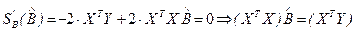
Таким образом, получим в матричной форме оценки параметров линейной регрессии:
 . (2.16)
. (2.16)
Для вычисления их не нужно составлять и решать нормальную систему линейных уравнений МНК. Достаточно выполнить указанные в формуле (2.16) алгебраические операции в матричной форме над результатами исходных, выборочных наблюдений X и Y. В частности, при выполнении контрольной работы такие расчеты достаточно легко выполняются с помощью Мастера функций табличного процессора Microsoft Exel.
2.4. Интерпретация оценок параметров и уравнения
множественной линейной регрессии
Интерпретация – содержательное объяснение – результатов анализа экономического явления или объекта, представленного статистическими (выборочными данными), является одной их самых важных задач регрессионного анализа. Так, рассматривая полученные оценки параметров уравнения регрессии, можно сказать, изменение фактора  на одну единицу своего измерения ведет к изменению объясняемой переменной
на одну единицу своего измерения ведет к изменению объясняемой переменной  на
на 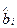 единиц измерения этой переменной. Направление ее изменения определяется знаком коэффициента перед фактором
единиц измерения этой переменной. Направление ее изменения определяется знаком коэффициента перед фактором  .
.
При этом единицы, в которых измерены выборочные значения переменных  и
и  , влияют на величину оценок параметров регрессии
, влияют на величину оценок параметров регрессии 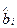 . Нужно обязательно фиксировать, в каких единицах измерены значения всех переменных, прежде чем заменять слово «единица» конкретными названиями: тонны, рубли и т.п. Отсюда следует, что коэффициенты регрессии перед различными факторами нельзя сравнивать друг с другом.
. Нужно обязательно фиксировать, в каких единицах измерены значения всех переменных, прежде чем заменять слово «единица» конкретными названиями: тонны, рубли и т.п. Отсюда следует, что коэффициенты регрессии перед различными факторами нельзя сравнивать друг с другом.
Все другие более общие показатели характера влияния факторов на объясняемую переменную, не зависящие от масштаба их измерения, такие как стандартизованные коэффициенты регрессии и коэффициенты эластичности, получают на основе этих оценок параметров  .
.
Параметр  представляет оценку значения объясняемой переменной
представляет оценку значения объясняемой переменной  при нулевых значениях факторных переменных. Она может иметь или не иметь экономический смысл в зависимости от характера конкретной ситуации.
при нулевых значениях факторных переменных. Она может иметь или не иметь экономический смысл в зависимости от характера конкретной ситуации.
При интерпретации модельного уравнения регрессии важно отмечать его следующие характерные особенности. Во-первых,  и
и  являются только оценками неизвестных констант
являются только оценками неизвестных констант  и
и  истинной, теоретической регрессии, которая к тому же не обязательно является линейной. Кроме того, величина и качество статистических оценок зависят от правильности выбора самого метода оценивания. В частности предпосылки МНК обосновывают условия, в которых можно получить «лучшие» оценки параметров модельной регрессии.
истинной, теоретической регрессии, которая к тому же не обязательно является линейной. Кроме того, величина и качество статистических оценок зависят от правильности выбора самого метода оценивания. В частности предпосылки МНК обосновывают условия, в которых можно получить «лучшие» оценки параметров модельной регрессии.
Во-вторых, эмпирическое уравнение регрессии отражает общую закономерную тенденцию, представленную выборочными данными, тогда как каждое отдельное наблюдение подвержено случайным воздействиям со стороны неконтролируемых факторов. Следовательно расчетные значения объясняемой переменной не могут быть детерминированными и их нужно дополнять характеристиками вариации, например, стандартными ошибками или доверительными интервалами.
И, наконец, в-третьих, правильность интерпретации зависит от правильного выбора и полноты модельного представления статистической связи. Это связано с включением в уравнение всех статистически значимых объясняющих переменных, а также выбором формы уравнения эмпирической функции регрессии. Если форма уравнения является линейной, то можно использовать такие характеристики линейной статистической связи, такие как коэффициенты парной, частной и множественной корреляции. Но в случае, когда реальная функция регрессии нелинейная, они не могут отражать силы влияния факторов.
3. Анализ качества уравнения регрессии
Выявление лучшего варианта эконометрической модели обычно осуществляется сравнением соответствующих им качественных характеристик, которые можно рассчитать на основе исходной статистической информации, содержащейся в векторе Y, матрице X, и новой расчетной информации, появляющейся после построении каждого из вариантов модели. Основным условием высокого «качества» модели является обоснованность математической формы уравнения эмпирической регрессии. Важную роль при этом играет как состав включенных в него независимых переменных, так и характер их взаимосвязей с зависимой переменной у, которые в совокупности определяют причины ее изменчивости.
Сопоставление новой расчетной информации, полученной после оценки параметров модельной регрессии с исходной статистической информацией позволяет установить, насколько удалось реализовать это условие на практике.
3.1. Характеристики и критерии качества эконометрических
моделей
Ведущая роль при определении характеристик качества эконометрической модели принадлежит ряду ее «выборочной» ошибки еi, i =1, 2,..., n, которая формируется с использованием найденных оценок ее параметров как
 ,
,
где  — расчетное значение переменной уi при известных значениях независимых переменных Xj ‑ xij, i = l, 2,..., n; j = 0, 1, 2, ..., p. Так для линейной модели (2.7) значения
— расчетное значение переменной уi при известных значениях независимых переменных Xj ‑ xij, i = l, 2,..., n; j = 0, 1, 2, ..., p. Так для линейной модели (2.7) значения  определяются на основании следующего выражения:
определяются на основании следующего выражения:

Для каждого набора оценок параметров  того или иного варианта модели, описывающей рассматриваемый процесс, рассчитывается «свой» ряд ошибки ei, который можно интерпретировать как ряд оценок ее истинных, но неизвестных значений e, теоретической регрессии (2.4).
того или иного варианта модели, описывающей рассматриваемый процесс, рассчитывается «свой» ряд ошибки ei, который можно интерпретировать как ряд оценок ее истинных, но неизвестных значений e, теоретической регрессии (2.4).
В общем случае «качество» эконометрической модели оценивается с помощью различных характеристик. Самой простой из них является средняя ошибка аппроксимации, которая вычисляется как среднее отклонение расчетных значений от результатов фактических измерений. Совокупность отклонений  можно рассматривать как абсолютные ошибки аппроксимации, а их абсолютные относительные величины
можно рассматривать как абсолютные ошибки аппроксимации, а их абсолютные относительные величины

как относительные ошибки аппроксимации.
Чтобы получить общее представление о качестве модели, из относительных отклонений по каждому наблюдению вычисляют среднюю ошибку аппроксимации  как простую среднюю арифметическую:
как простую среднюю арифметическую:
 (3.1)
(3.1)
Считается, что допустимый предел ошибки не должен превышать 8 – 10%.
Другой характеристикой качества модельного уравнения регрессии является несмещенная оценка дисперсии случайных отклонений  :
:
 (3.2)
(3.2)
где р – число объясняющих переменных, факторов. Корень квадратный из оценки дисперсии обозначается как Se и называется стандартной ошибкой регрессии.
Ошибка модельной регрессии во многом предопределена тем, что оценки  рассчитывают по данным случайных измерений, и они являются случайными значениями величин b0, b1, ,bР ‑ неизвестных коэффициентов регрессии. Насколько хорошим оказывается соответствие между ними, насколько приемлемым можно считать «качество» полученной модели регрессии.
рассчитывают по данным случайных измерений, и они являются случайными значениями величин b0, b1, ,bР ‑ неизвестных коэффициентов регрессии. Насколько хорошим оказывается соответствие между ними, насколько приемлемым можно считать «качество» полученной модели регрессии.
Надежность случайных оценок устанавливают также с помощью определения оценок их дисперсий (стандартных ошибок). Кроме того, строят доверительные интервалы для теоретических значений и проверяют статистические гипотезы о значимости отличия их эмпирических величин от ожидаемых, теоретических значений.
3.2. Дисперсии и стандартные ошибки параметров линейной регрессии
Оценки коэффициентов множественной линейной регрессии в матричной форме (2.2) определяются следующим образом:
 .
.
Чтобы оценить ошибку оценки матрицы коэффициентов регрессии  подставим в правую часть формулы теоретические значения объясняемой переменной
подставим в правую часть формулы теоретические значения объясняемой переменной 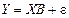 :
:

Таким образом, ошибка полученной оценки  имеет вид:
имеет вид:
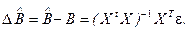
Дисперсия многомерной случайной величины  определяется с помощью ковариационной матрицы
определяется с помощью ковариационной матрицы  :
:

В силу того, что объясняющие переменные XJ не являются случайными величинами, их можно вынести за знак математического ожидания:
 (3.4)
(3.4)
Матрица  представляет собой ковариационную матрицу неизвестных случайных отклонений e теоретической регрессии:
представляет собой ковариационную матрицу неизвестных случайных отклонений e теоретической регрессии:
 .
.
В силу предпосылки МНК 2° все диагональные элементы одинаковы  , а все остальные равны нулю в силу предпосылки 3°. Таким образом, ковариационная матрица случайных ошибок
, а все остальные равны нулю в силу предпосылки 3°. Таким образом, ковариационная матрица случайных ошибок  =
=  , а выражение (3.4) принимает следующий вид:
, а выражение (3.4) принимает следующий вид:
 (3.5)
(3.5)
Неизвестное значение дисперсии случайного отклонения теоретической регрессии  заменяется соответствующей несмещенной выборочной оценкой
заменяется соответствующей несмещенной выборочной оценкой  (3.2). Следовательно, по выборке мы можем определить только выборочные оценки дисперсий коэффициентов эмпирической регрессии
(3.2). Следовательно, по выборке мы можем определить только выборочные оценки дисперсий коэффициентов эмпирической регрессии  , которые являются диагональными элементами матрицы
, которые являются диагональными элементами матрицы  :
:
 , (3.6)
, (3.6)
где через  обозначены диагональные элементы обратной матрицы
обозначены диагональные элементы обратной матрицы  , j = 0, 1, 2, ..., p.
, j = 0, 1, 2, ..., p.
Стандартные ошибки коэффициентов регрессии вычисляются по формулам:
 , (3.7)
, (3.7)
где j = 0, 1, ..., p.
3.3. Доверительные интервалы коэффициентов регрессии
Для построения интервальной оценки неизвестных коэффициентов регрессии  вводится случайная величина
вводится случайная величина  - стандартизованный коэффициент регрессии, имеющая распределение Стьюдента с числом степеней свободы
- стандартизованный коэффициент регрессии, имеющая распределение Стьюдента с числом степеней свободы  .
.
При заданном уровне значимости a доверительный интервал записывается следующим образом:

где  - табличное значение t-критерия Стьюдента
- табличное значение t-критерия Стьюдента
Из данного неравенства следует:

 (3.8)
(3.8)
где  и
и  - стандартная и предельная ошибки выборочных оценок
- стандартная и предельная ошибки выборочных оценок 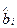 соответственно.
соответственно.
3.4. Стандартная ошибка и доверительные интервалы уравнения регрессии
Дисперсия многомерной случайной величины  определяется с помощью ковариационной матрицы
определяется с помощью ковариационной матрицы  :
:

где матрица  определена формулой (3.6).
определена формулой (3.6).
Таким образом, получаем окончательное выражение в матричной форме:
 (3.9)
(3.9)