Оценка коэффициентов модели регрессии с гетероскедастичными остатками

Для проверки гипотезы о наличии гетероскедастичности используются различные тесты, одним из часто используемых является тест Уайта.

Для проведения теста необходимо сначала построить регрессионную модель обычным МНК и далее выбрать тест Уайта из списка, нажав Тесты – Гетероскедастичность.

Рисунок 7 - Результаты оценки модели регрессии

При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой некоторую функцию от наблюдаемых значений факторного признака (признаков), т.е.

Чаще всего функция f выбирается квадратичной, что соответствует тому, что средняя квадратическая ошибка регрессии зависит от наблюдаемых значений регрессоров приближенно линейно[1]. Гомоскедастичной выборке соответствует случай f=const.

Идея теста Уайта заключается в оценке функции fс помощью соответствующего уравнения регрессии для квадратов остатков:

где — случайный член.

При справедливости гипотезы об отсутствии гетероскедастичности величина асимптотически имеет распределение , ( — коэффициент детерминации, а — число регрессоров во второй модели регрессии).

Проведем тест Уайта на гетероскедастичность для факторных признаков Х7,Х8 и Х4.

Рисунок 8 - Результаты проверки по тесту Уайта

Отметим, что значимым оказался коэффициент при Х7 , Х7² и Х8², то есть можно ожидать, что дисперсия остатков пропорциональна факторной переменной Х7 и пропорциональна квадратам переменных Х7 и Х8.

Замечание: Программа автоматически извлекает корень из весов при реализации взвешенного метода наименьших квадратов

Для устранения гетероскедастичности можем использовать взвешенный МНК с весами:

,

где

- модельное значение уравнения регрессии квадратов регрессионных остатков на факторные признаки, их квадраты и попарные произведения, то есть .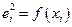

Необходимо отметить, что программа Gretl автоматически извлекает корень из весов при реализации взвешенного метода наименьших квадратов, поэтому нам понадобится только сохранить как переменную и преобразовать ее в весовую переменную . Для определения весов сначала найдем (переменная W), вычислив новую переменную по формуле (Рисунок 9).

Рисунок 9 - Вычисление переменной W.

Далее вычислим непосредственно вес (Рисунок 10).

Рисунок 10 – Описание переменных для анализа

Далее строим регрессионную модель с помощью Взвешенного МНК, выбирая в основном меню Модели – Другие линейные модели – Взвешенный МНК. В открывшемся диалоговом окне устанавливаем опции как показано на Рисунке 11.

Рисунок 11 - диалоговое окно Спецификация модели

В итоге получим следующие результаты (Рисунок 12).

Рисунок 12 - Результаты оценки модели взвешенным МНК

Проанализируем полученные результаты, сравнив их с предыдущей моделью (Рисунок 7). Заметим, что обе модели являются значимыми, в этих двух моделях коэффициент детерминации равен 0,34 при одной значимой переменной Х8.