Определения. Парная регрессия. Метод наименьших квадратов (МНК).

Если формула (3) линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией, зависимость от нескольких переменных – множественной регрессией. Например, Кейнсом была предложена линейная модель зависимости частного потребления С от располагаемого дохода Х: С=С₀+ С₁Х, где С₀ >0 – величина автономного потребления (при уровне дохода Х=0), 1>C₁>0 – предельная склонность к потреблению (C₁ показывает, на сколько увеличится потребление при увеличении дохода на единицу).

В случае парной линейной регрессии имеется только один объясняющий фактор х и линейная регрессионная модель записывается в следующем виде:

у=a₀+a₁х+e, (4)

где e – случайная составляющая с независимыми значениями Мe=0, De= s².

Оценка параметров регрессии a₀ и a₁ производится по наблюденным значениям зависимой и объясняющей переменным (x_i,y_i), i=1,2,…,n, где n – число пар наблюдений (объем выборки). Рассматриваются n уравнений у_i=a₀+a₁х_i+e_i, где уклонения e_i является следствием реализации случайной составляющей, и выбирают такие значения a₀ и a₁, которые минимизируют сумму квадратов этих уклонений, т.е. ищется минимум

Q=å_ie_i²= å_i(у_i – a₀ – a₁х_i)² (5)

по отношению к параметрам a₀ и a₁. Заметим, что указанный метод наименьших квадратов (МНК)может быть применен к любой кривой регрессии f(x). “Наилучшая” по МНК прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость у= f(x) является, например, квадратичной, то ее не сможет адекватно описать никакая линейная функция, хотя среди всех линейных функций обязательно найдется “наилучшая”.

Для отыскания минимума берутся частные производные Q по искомым параметрам (в данном случае по a₀ и a₁) и приравниваются к нулю. После выполнения элементарных преобразований получают так называемую систему нормальных уравнений, из которой и находятся искомые параметры. Для парной линейной регрессии получаем

a₁=( 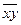– 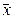× 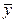)/( – ( 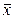)²), (6)

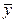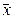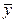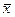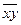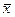a₀= –a₁ × =(( ) × – × )/( – ( )²),

где 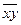=åx_iy_i/n, 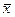=åx_i/n, 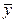=åy_i/n, =åх_i²/n.

Коэффициент a₁ называется коэффициентом регрессии и обозначается r_yx. Из (2) и (6) следует, что

r_yx = r_yx s_y /s_х. (7)

Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (репрезентативна), то заключение о тесноте линейной зависимости между признаками, полученными по данным выборки, в известной степени может быть распространено и на генеральную совокупность, т.е. можно выдвинуть гипотезу об имеющейся линейной связи во всей генеральной совокупности вида у=a₀+a₁х.