Использование регрессионной модели для прогноза. Дисперсия ошибки прогноза.

Основное назначение регрессионной модели – использование ее для прогноза экономического показателя Y. Прогноз осуществляется подстановкой значения фактора в оценку детерминированной составляющей:

. (2.5.16)

Построим доверительный интервал для функции регрессии, т. е. для условного математического ожидания М(Y/x_l), который с заданной надежностью (доверительной вероятностью) Р=1- 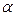накрывает неизвестное значение М(Y/x_l).

Найдем дисперсию прогноза , представляющего собой выборочную оценку М(Y/x_l). С этой целью уравнение (2.5.16) представим в виде:

 

. (2.5.17)

 

Дисперсия равна сумме дисперсий двух независимых (доказательство этого факта опускается) слагаемых выражения (2.5.17).

 

(2.5.18)

 

Здесь учтено, что – неслучайная величина, при вынесении которой за знак дисперсии ее необходимо возвести в квадрат.

Дисперсия выборочной средней

 

 

(2.5.19)

Для нахождения дисперсии воспользуемся формулой (2.5.15), т.е.

Найдем оценку дисперсии , учитывая (2.5.18), (2.5.19), (2.5.15) и заменяя ее оценкой .

 

(2.5.20)

 

Основываясь на предпосылках 1-5 регрессионного анализа, можно показать, что статистика

 

 

имеет распределение Стьюдента с ν=n-2 степенями свободы и построить доверительный интервал для условного математического ожидания

 

(2.5.21)

 

Из формул (2.5.20) и (2.5.21) видно, что величина доверительного интервала зависит от значения объясняющей переменной : при она минимальна, а по мере удаления от величина доверительного интервала увеличивается.

Ошибку прогноза можно представить следующим образом

(2.5.22)

Первая скобка представляет собой ошибку, вызванную наличием случайной составляющей ε. Ее дисперсия равна .

Вторая скобка представляет собой ошибку оценки среднего уровня. Ее дисперсия определяется по формуле (2.5.20).

Таким образом, для оценки дисперсии ошибки прогноза можно пользоваться следующим выражением

. (2.5.23)

Эта формула учитывает как погрешность оценки так и отклонение от своего математического ожидания, обусловленное наличием случайной составляющей.

Из (2.5.23) следует, что с ростом дисперсия ошибки прогноза увеличивается.