Тема Множественная регрессия (Задачи)
Уравнение регрессии, построенное по 15 наблюдениям, имеет вид:

Пропущенные значения, а также доверительный интервал для
 с вероятностью 0,99 равны:
с вероятностью 0,99 равны:
+— 
— 
— 
— 
Уравнение регрессии, построенное по 20 наблюдениям, имеет вид:

Пропущенные значения, а также доверительный интервал для  с вероятностью 0,9 равны:
с вероятностью 0,9 равны:
+— 
— 
— 
— 
Уравнение регрессии, построенное по 16 наблюдениям, имеет вид:

Пропущенные значения, а также доверительный интервал для  с вероятностью 0,99 равны:
с вероятностью 0,99 равны:
+— 
— 
— 
— 
Уравнение регрессии в стандартизированном виде имеет вид:


Частные коэффициенты эластичности равны:
|

Уравнение регрессии в стандартизированном виде имеет вид:


|

Стандартизованное уравнение регрессии имеет вид:


Частные коэффициенты эластичности равны:
|

Стандартизованное уравнение регрессии имеет вид:


|

Стандартизованное уравнение регрессии имеет вид:


|

Стандартизованное уравнение регрессии имеет вид:


|

Стандартизованное уравнение регрессии имеет вид:


Частные коэффициенты эластичности равны:
|

По 18 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 17 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 22 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 25 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 24 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 28 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 26 наблюдениям получены следующие данные:

 ;
;  ;
;  ;
;  ;
; 
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
В уравнении регрессии: 

Восстановить пропущенные характеристики; построить доверительный интервал для  с вероятностью 0,95, если n=12
с вероятностью 0,95, если n=12
+— 

 (-12,02;-2,98)
(-12,02;-2,98)
— 

 (-12,02;-2,98)
(-12,02;-2,98)
— 

 (-11,12;-3,88)
(-11,12;-3,88)
— 

 (-11,12;-3,88)
(-11,12;-3,88)
Уравнение регрессии в стандартизованном виде имеет вид:


Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+—Наибольшее влияние на результат оказывает фактор  , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее -  ;
; 


—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



Уравнение регрессии в стандартизованном виде имеет вид:


Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+—Наибольшее влияние на результат оказывает фактор  , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее -  ;
; 


—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



Уравнение регрессии в стандартизованном виде имеет вид:


Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+—Наибольшее влияние на результат оказывает фактор  , наименьшее
, наименьшее 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее -  ;
; 


—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



—Наибольшее влияние на результат оказывает фактор  наименьшее -
наименьшее - 



По 20 наблюдениям получены следующие данные:

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 
По 16 наблюдениям получены следующие данные:

Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра  равны:
равны:
+— 
— 
— 
— 







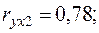
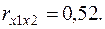 Уравнения регрессии
Уравнения регрессии 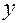 на
на 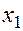 и
и  в стандартизованном и натуральном масштабе имеют вид:
в стандартизованном и натуральном масштабе имеют вид:
+— 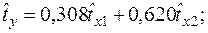
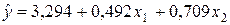
— 
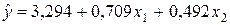
— 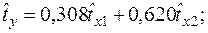
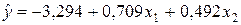
— 
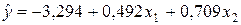
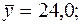
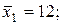
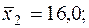
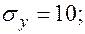
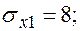
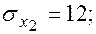
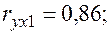
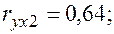
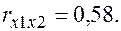 Уравнения регрессии y на
Уравнения регрессии y на 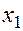 и
и  в стандартизированном и натуральном масштабе имеют вид:
в стандартизированном и натуральном масштабе имеют вид:
+— 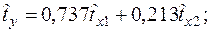
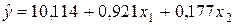
— 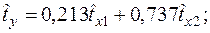
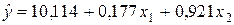
— 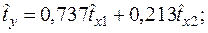
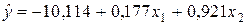
— 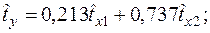
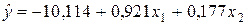
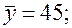

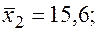
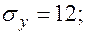
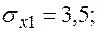
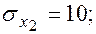

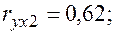
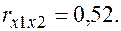 Уравнения регрессии
Уравнения регрессии 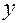 на
на 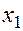 и
и  в стандартизованном и натуральном масштабе имеют вид:
в стандартизованном и натуральном масштабе имеют вид:
+— 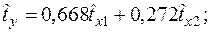
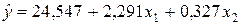
— 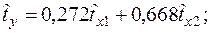
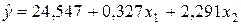
— 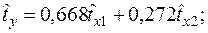

— 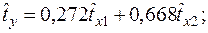
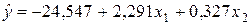

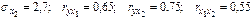 . Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
. Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 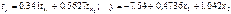
— 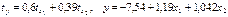
— 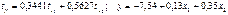
— 
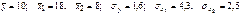
 . Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
. Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 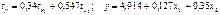
— 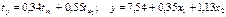
— 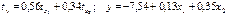
— 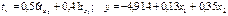
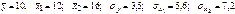
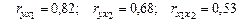 . Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
. Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 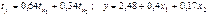
— 
— 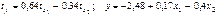
— 
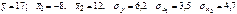
 .Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
.Уравнения регрессии в стандартизированном и натуральном масштабе имеют вид:
+— 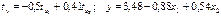
— 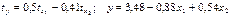
— 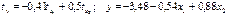
— 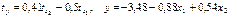
При построении регрессионной зависимости некоторого результативного признака на 8 факторов по 25 измерениям коэффициент детерминации составил 0,736. После исключения 3 факторов коэффициент детерминации уменьшился до 0,584. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровнях 0,05 и 0,01
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровне 0,01
—Да, только на уровнях 0,1 и 0,05
При построении регрессионной зависимости некоторого результативного признака на 7 факторов по 32 измерениям коэффициент детерминации составил 0,812. После исключения 2 факторов коэффициент детерминации уменьшился до 0,76. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровнях 0,05 и 0,01
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровне 0,01
—Да, только на уровнях 0,1 и 0,05
При построении регрессионной зависимости некоторого результативного признака на 10 факторов по 45 измерениям коэффициент детерминации составил 0,617. После исключения 3 факторов коэффициент детерминации уменьшился до 0,512. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровне 0,01
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровнях 0,05 и 0,01
—Да, только на уровнях 0,1 и 0,05
При построении регрессионной зависимости некоторого результативного признака на 10 факторов по 45 измерениям коэффициент детерминации составил 0,347. После добавления 3 факторов коэффициент детерминации увеличился до 0,536. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровнях 0,1 и 0,05
—Да, только на уровне 0,1
—Да, только на уровнях 0,05 и 0,01
При построении регрессионной зависимости некоторого результативного признака на 7 факторов по 42 измерениям коэффициент детерминации составил 0,443. После добавления 3 факторов коэффициент детерминации увеличился до 0,527. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Нет, на всех уровнях значимости
—Да, на всех уровнях значимости
—Да, только на уровнях 0,1 и 0,05
—Да, только на уровне 0,1
—Да, только на уровнях 0,05 и 0,01
При построении регрессионной зависимости некоторого результативного признака на 8 факторов по 38 измерениям коэффициент детерминации составил 0,558. После добавления 2 факторов коэффициент детерминации увеличился до 0,644. Обоснованно ли было принятое решение на уровнях значимости 0,1, 0,05 и 0,01:
+—Да, только на уровнях 0,1 и 0,05
—Да, на всех уровнях значимости
—Нет, на всех уровнях значимости
—Да, только на уровне 0,1
—Да, только на уровнях 0,05 и 0,01
По данным 150 наблюдений о доходе индивидуума Y, уровне его образования X1, и возрасте X2 определите, можно ли считать на уровне значимости 5 % линейную регрессионную модель Y на X1 и X2 гетероскедастичной, если суммы квадратов остатков после упорядочения данных по уровню образования следующие: RSS1 (для 50 значений с наименьшим уровнем образования) = 894,1; RSS2 (для 50 значений с наибольшим уровнем образования) = 3918,2:
+—гипотеза об отсутствии гетероскедастичности отвергается
—гипотеза об отсутствии гетероскедастичности принимается
—на основе имеющихся данных такую гипотезу нельзя проверить
Имеется следующая модель, построенная на основе 30 наблюдений:
Y = 1, 48+ 0, 788X R2 = 0,97
(3,29) (29,37)
В скобках указаны t – статистики
Для проверки гетероскедастичности, были построены отдельные модели по первым 12 и последним 12 наблюдениям. Остаточные суммы квадратов отклонений составили RSS1 = 1069 и RSS2 = 3344 . Проверить гипотезу о гомоскедастичности с уровнем значимости 5%:
+—гипотеза о гомоскедастичности отвергается
—гипотеза о гомоскедастичности принимается
—для проверки данной гипотезы в данной задаче недостаточно данных
Имеется следующая модель, построенная на основе 30 наблюдений:
Y = 1, 75+ 1, 251X R2 = 0,97
(3,02 ) (2,37)
В скобках указаны t – статистики
Для проверки гетероскедастичности, были построены отдельные модели по первым 12 и последним 12 наблюдениям. Остаточные суммы квадратов отклонений составили RSS1 = 344 и RSS2 = 769 . Проверить гипотезу о гомоскедастичности с уровнем значимости 5%:
—гипотеза о гомоскедастичности отвергается
+—гипотеза о гомоскедастичности принимается
—для проверки данной гипотезы в данной задаче недостаточно данных