ГЛОССАРИЙ
Автокорреляция– корреляция между временной переменной и лаговой переменной, составленной от той же переменной.
Авторегрессия– регрессия зависимой временной переменной от лаговой переменной, составленной от той же переменной.
Адаптивные полиномиальные модели– адаптивные модели временного ряда, основанные на представлении уровней ряда в виде полиномов от интервала прогнозирования.
Аддитивная модель - имеет вид: Y=T+S+E;
Белый шум– стохастический процесс, представляющий собой последовательность независимых, одинаково распределенных случайных величин.
Временной ряд (ряд динамики, динамический ряд)– упорядоченная во времени последовательность численных показателей {(yi,ti), i = 1, 2, ..., n}, характеризующих уровни развития изучаемого явления в последовательные моменты или периоды времени.
Выборочная ковариация – является мерой взаимосвязи между двумя переменными.
Гетероскедастичность– неоднородность относительно дисперсии.
Гладкость ряда означает отсутствие случайных, сезонных или циклических колебаний.
Гомоскедастичность– однородность относительно дисперсии.
Двухшаговый метод наименьших квадратов– применяется для оценки параметров сверхидентифицируемой системы уравнений.
Доверительным называют интервал, который покроет неизвестный параметр с заданной надежностью.
Интервальный прогноз– интервал, в котором с определенной вероятностью находится фактическое значение прогнозируемой переменной.
Коинтеграция нестационарных временных рядов– возможность получить стационарную линейную комбинацию исходных нестационарных временных рядов.
Конкурирующей (альтернативной) (H1) называют гипотезу, которая противоречит нулевой.
Корреляционная связь– зависимость, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Корреляционный анализ– раздел математической статистики, изучающий наличие и тесноту связи между переменными без разделения переменных на зависимые и объясняющие.
Косвенный метод наименьших квадратов– применяется для оценки параметров идентифицируемой системы уравнений.
Коэффициент детерминации R2– представляет собой квадрат коэффициента корреляции, показывает, какая часть дисперсии результативного признака объяснена уравнением регрессии.
Коэффициент корреляции- мера взаимосвязи между явлениями.
Коэффициент эластичности Э – для зависимости 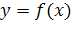 вычисляется по формуле:
вычисляется по формуле: 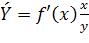 , показывает, на сколько процентов в среднем изменится результативный признак у при изменении фактора х на 1 % от своего номинального значения.
, показывает, на сколько процентов в среднем изменится результативный признак у при изменении фактора х на 1 % от своего номинального значения.
Критерий Стьюдента (t-критерий)– применяется для оценки статистической значимости коэффициентов полученного уравнения регрессии.
Критерий Фишера (F-критерий)– применяется для оценки статистической значимости полученного уравнения регрессии в целом.
Критерий Энгеля-Грэнджера– применяется для тестирования временных рядов на коинтеграцию.
Критические точки – это точки, отделяющие критическую область от области принятия гипотезы.
Критической областью называют совокупность значений критерия, при которых нулевая гипотеза отвергается.
Лаг– задержка. Обычно лаг рассматривают между причиной и следствием.
Линейная аналитическая зависимость– зависимость, определяемая соотношением 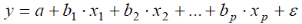 .
.
Линейный коэффициент корреляцииryx – характеризует тесноту линейной связи между переменными 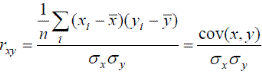
Логистическая аналитическая зависимость– зависимость, определяемая соотношением 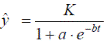
Ложная корреляция– высокое значение коэффициентов корреляции при отсутствии истинной зависимости между переменными.
Математическое ожидание– это среднее значение по генеральной совокупности.
Метод Алмон– применяется для оценки коэффициентов модели с распределенным лагом. Согласно методу Алмон, коэффициенты представляются в виде полиномов заданной степени k от величины лага j: 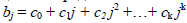 .
.
Метод аналитического выравнивания– заключается в нахождении аналитической функции ŷ = f(t), характеризующей основную тенденцию (тренд) изменения уровней временного ряда с течением времени.
Метод включения– применяется при отборе факторов множественной регрессии. Согласно методу включения, сначала строится уравнение регрессии с одним наиболее влияющим фактором (фактор, которому соответствует большее значение парного коэффициента корреляции с результативным признаком ( 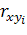 ), затем уравнение регрессии с двумя наиболее влияющими факторами и т. д.
), затем уравнение регрессии с двумя наиболее влияющими факторами и т. д.
Метод исключения– применяется при отборе факторов множественной регрессии. Согласно методу исключения сначала строится уравнение регрессии с полным набором факторов, из числа которых затем последовательно исключаются наименее значимые факторы.
Метод Койка– применяется для оценки параметров модели с распределенным лагом. Основан на предположении, что коэффициенты при лаговых переменных убывают в геометрической прогрессии.
Метод наименьших квадратов (МНК)– метод оценки параметров уравнения регрессии, основанный на минимизации суммы квадратов отклонений расчетных значений (по уравнению регрессии) зависимой переменной от ее наблюдаемых значений.
Метод сравнения средних– применяется для выявления наличия монотонной тенденции на основе сравнения средних уровней двух отрезков временного ряда.
Метод Фостера-Стюарта– непараметрический метод, применяемый для выявления наличия монотонной тенденции временного ряда.
Модели авторегрессии– динамические модели, определяемые соотношением 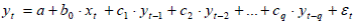 .
.
Модели с распределенным лагом– динамические модели, определяемые cоотношением 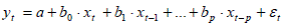 .
.
Модель адаптивных ожиданий– динамическая модель, основанная на предположении, что фактическое значение переменной yt формируется под воздействием ожидаемого значения объясняющей переменной 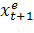 в следующий момент времени.
в следующий момент времени.
Модель частичной корректировки– динамическая модель, основанная на предположении, что под воздействием объясняющей переменной xt формируется не фактическое значение переменной yt, а ее «желаемый» уровень y*t.
Мультиколлинеарность– множественная линейная связь. Мультиколлинеарность обозначает коррелированность двух или нескольких объясняющих переменных в уравнении регрессии.
Мультипликативная модель: Y=T∙S∙E.
Наблюдаемым значением называют значения критерия, вычисленного по выборкам.
Непараметрические тесты стационарности– тесты на стационарность, не выдвигающие каких-либо предположений о законе распределения тестируемого временного ряда, его параметрах.
Нормальное распределение определяется двумя параметрами: средним квадратическим отклонением s и математическим ожиданием a.
Нормальную кривую называют кривой Гаусса. Кривая Гаусса всегда симметрична, все центральные тенденции равны. Асимметрия, эксцесс. Вероятность попадания в заданный интервал нормальной случайной величины определяется при помощи функции Лапласа.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью.
Нормированнымназывают нормальное распределение со средним квадратическим отклонением равным единице и математическим ожиданием равным нулю.
return false">ссылка скрытаНулевой гипотезой (H0) называют выдвинутую гипотезу.
Областью принятия гипотезы (область допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.
Обобщенный метод наименьших квадратов– метод оценки параметров уравнения регрессии, в котором МНК применяется к уравнению регрессии, преобразованному таким образом, чтобы исключить гетероскедастичность остатков.
Остаточная дисперсия– величина, вычисляемая по формуле 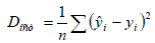 , где
, где 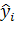 , yi – расчетное и наблюдаемое значение зависимой переменной.
, yi – расчетное и наблюдаемое значение зависимой переменной.
Оценка называется несмещенной, если математическое ожидание, рассчитанное по выборке, равно соответствующей характеристике генеральной совокупности.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Параметрические тесты стационарности– тесты на стационарность, основанные на относительно строгих предположениях относительно законов распределения временного ряда, его параметров.
Плотности распределения непрерывных случайных величин называют законами распределения.
Плотность распределения вероятностей непрерывной случайной величины называют функцию f (x) – первую производную от функции распределения F (x).
Показательная аналитическая зависимость– зависимость, определяемая соотношением ŷ = a·bx.
Поле корреляций– совокупность точек на координатной плоскости, изображающих наблюдения.
Полулогарифмическая аналитическая зависимость– зависимость, определяемая соотношением 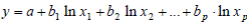 .
.
Правило принятия решения для проверки статистических гипотез – это модель расчета значений выборочных статистических показателей, на основании которых принимается или отвергается нулевая гипотеза.
Предмет эконометрики– количественная оценка взаимосвязи между случайными событиями, признаками, показателями, факторами переменных экономических объектов.
Приведенная форма модели– система одновременных уравнений, которая отражает зависимость эндогенных переменных только от предопределенных переменных.
Простой гипотизойназывают гипотезу, содержащую только одно предположение.
Равномерным распределение вероятностей называют, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Ранговая корреляция отражает статистическую связь между порядковыми переменными.
Ранжировка- последовательность рангов элементов вариационного ряда, указывающих на место объекта в ряду.
Регрессионный анализ– раздел математической статистики, изучающий форму зависимости характеристик стохастического процесса от одного или нескольких факторов.
Регрессия– зависимость среднего значения какой-либо величины (y) от некоторой другой величины или от нескольких величин (хi).
Регрессия множественная– зависимость с несколькими зависимыми переменными.
Регрессия парная– зависимость между двумя переменными.
Результативный признак– признак, изменяющийся под действием факторных признаков.
Сложная гипотеза – это гипотеза, которая состоит из двух или нескольких простых гипотез
Случайная величина – действительная переменная, которая в зависимости от исхода опыта, т.е. в зависимости от случая, принимает различные значения.
Случайное блуждание– стохастический процесс, определяемый соотношением Yt = Yt–1 + εt.
Состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в нее конкретных наблюдений.
Средняя квадратическая ошибка модели– величина, вычисляемая по формуле 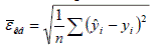 , где
, где 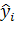 , yi – расчетное и наблюдаемое значение зависимой переменной.
, yi – расчетное и наблюдаемое значение зависимой переменной.
Статистическая гипотеза – это гипотеза о виде неизвестного распределения, или о параметрах известных распределений.
Статистическим критерием называют случайную величину, которая служит для проверки нулевой гипотезы.
Статистической оценкой неизвестного параметра теоретического распределения называют его приближенное значение, зависящее от данных выборки, т.е. некоторую функцию этих величин.
Стационарный стохастический процесс в узком (сильном) смысле– стохастический процесс, для которого совместное распределение вероятностей случайных величин Xt , Xt ,..., Xtn 1 2 такое же, как у случайных величин 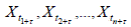 при любых n, t и τ.
при любых n, t и τ.
Стационарный стохастический процесс в широком (слабом) смысле– стохастический процесс, у которого математическое ожидание μt и дисперсия σ2t не зависят от времени (одинаковы для всех Xt), а автоковариация 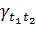 зависит только от величины лага τ = t2–t1.
зависит только от величины лага τ = t2–t1.
Степенная аналитическая зависимость– зависимость, определяемая соотношением 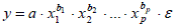
Стохастическая связь– причинная зависимость, которая проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений.
Стохастический– случайный, вероятностный.
Стохастический процесс– случайная функция X(t) вещественного аргумента t.
Структурная форма модели– исходная система одновременных уравнений, содержащая в качестве факторов зависимые переменные.
Тенденция– изменение, определяющее общее направление развития, основную тенденцию временного ряда.
Теорема Гаусса-Маркова– теорема, определяющая условия, при соблюдении которых оценки параметров линейной регрессии, полученные методом наименьших квадратов, будут несмещенными и эффективными в классе линейных несмещенных оценок
Тест Глейзера– применяется для проверки остатков регрессии на гетероскедастичность. Проверяет существование функциональной зависимости следующего вида 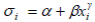
Тест Гольдфельда–Квандта– применяется для проверки остатков регрессии на гетероскедастичность. Проверяет равенство дисперсий остатков на двух интервалах изменения фактора.
Тест Дики-Фуллера– применяется для тестирования временного ряда на нестационарность, основан на оценке параметра λ=α1–1 уравнения ΔYt=λ·Yt–1+εt.
Тест Манна-Уитни– непараметрический тест стационарности применяется для тестирования постоянства математического ожидания и основан на сопоставлении рангов элементов двух совокупностей из рассматриваемого интервала.
Тест на единичный корень (тест Дики-Фуллера)– применяется для тестирования временного ряда на нестационарность, основан на оценке параметра λ = α1–1 уравнения ΔYt = λ·Yt–1 + εt.
Тест ранговой корреляции Спирмена– применяется для проверки остатков регрессии на гетероскедастичность. Проверяет наличие монотонной зависимости между дисперсией ошибки и величиной фактора.
Тест Сиджела-Тьюки– применяется для тестирования постоянства дисперсии временного ряда и основан на сопоставлении рангов элементов двух совокупностей из рассматриваемого интервала.
Точечный прогноз– среднее прогнозное значение изучаемой переменной экономического объекта.
Тренд– изменение, определяющее общее направление развития, основную тенденцию временного ряда.
Трехшаговый метод наименьших квадратов– применяется для оценки параметров системы уравнений при нарушении предпосылок о независимости и гомоскедастичности остатков системы одновременных уравнений.
Условия Гаусса-Маркова– условия, обеспечивающие состоятельность, несмещенность и эффективность оценок параметров уравнения регрессии с помощью МНК.
Факторный признак– признак, обуславливающий изменение другого, связанного с ним признака.
Фиктивные переменные– применяются для учета в модели влияния качественного фактора.
Функциональная связь– связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Функция распределения вероятностей случайной величины – функция, определяющая вероятность того, что случайная величина Х в результате испытания примет значение, меньшее Х.
Частные уравнения регрессии– характеризующие изолированное влияние одного из факторов хi на результативную переменную y при исключении влияния остальных факторов, входящих в общее уравнение регрессии.
Экзогенные (внешние, независимые) переменные– переменные, значения которых определяются вне рассматриваемой модели, для которой они являются заданными.
Эконометрика– раздел науки, изучающий конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей.
Экспоненциальная аналитическая зависимость– зависимость, определяемая соотношением 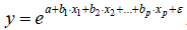
Экспоненциальное сглаживание – сглаживание временного ряда уt на основе рекуррентной формулы 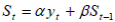 , где St – значение экспоненциальной средней в момент t; уt – значение временного ряда в момент t; α – параметр сглаживания, α = const, 0< α <l; β = 1– α .
, где St – значение экспоненциальной средней в момент t; уt – значение временного ряда в момент t; α – параметр сглаживания, α = const, 0< α <l; β = 1– α .
Экстраполяция– прогноз, получение расчетных значений при условии, что значения аргумента выходят за пределы области определения функции.
Эндогенные (внутренние, зависимые) переменные– переменные, значения которых определяются внутри рассматриваемой модели.