Построение моделей регрессии

 

Судя по корреляционной матрице, связи между зависимой переменной Y и всеми независимыми переменными Х значимы. Получаем следующие варианты моделей парной регрессии:

1) ;

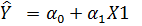2) ;

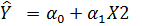3) ;

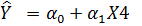4) .

 

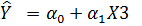Варианты моделей множественной регрессии:

5) 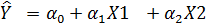(хотя в этой модели Y связан с факторами теснее, чем факторы друг с другом, влияние мультиколлинеарности все же может проявиться)

6) .

 

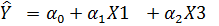Построим модели множественной регрессии и сравним полученные результаты в таблицах 3 и 4.

 

Из таблицы 2 видно, что переменные X1_X3 и X3_X4 значимы.

При построении всех моделей для повышения R-squared были исключены наблюдения, у которых остатки превышали по модулю 3.

Для устранения гетероскедастичности в моделях использовался взвешенный метод наименьших квадратов (введена новая переменная
W= 1/sqrt(X_norm))

 

Таблица 2.Характеристики информационной пригодности и значимость параметров конкурирующих моделей

Модель	R2, % R-squared	Исправленный R2, %	F-статистика F-Ratio	Станд. ошибка. модели
№	Запись в явном виде
	Y_norm = 0,3778 +0,5178*X1_norm (3,2127) (5,11772)	49,2396	47,3596	26,19	0,528753
	Y_norm = 0,3329+1,5871*X3_norm (2,7774) (4,9028)	50,0384	47,9567	24,04	0,509455
	Y_norm = 0,6295-0,4076*X4_norm (5,4045) (-2,6743)	21,5728	18,5564	7,15	0,6143
	Y_norm = 0,3472+ 1,3292*X1_norm (2,9887) (4,2491) + 0,1587*X3_norm (1,5702)	53,6364	50,0699	15,04	0,514961
	Y_norm = 0,3301+ 0,2856*X3_norm (4,6013) (4,7457) - 0,4478*X4_norm (-5,3617)	71,5246	68,8126	26,37	0,325399

 

 

Таблица 3. Показатели для выявления ошибок спецификации конкурирующих моделей

Модель	Статистика Дарбина-Уотсона	Корреляция остатков и ведущего фактора
№	Запись в явном виде
	Y_norm = 0,3778 +0,5178*X1_norm	1,55955 (P=0,1185)	0,0034 (0)
	Y_norm = 0,3329+1,5871*X3_norm	2,32884 (P=0,7951)	0,0105 (0)
	Y_norm = 0,6295 - 0,4076*X4_norm	1,5788 (P=0,1146)	0(0)
	Y_norm = 0,3472+ 1,3292*X1_norm + 0,1587*X3_norm	1,87115 (P=0,3548)	0,006 (0,0002; 0,1285)
	Y_norm = 0,3301+ 0,2856*X3_norm - 0,4478*X4_norm	2,76483 (P=0,9663)	0,0002 (0,0001;0)