Нормирование переменных.

Чтобы устранить влияние разных единиц измерения и облегчить интерпретацию моделей, нормируем значения переменных, разделив их на стандартные отклонения.

Хi_norm=Xi/δx

 

Наблюдения, признанные аномальными при расчете стандартного отклонения не учитываем.

Пронормируем переменные по следующим формулам:

Y_norm=SELECT(Y;SELECTED)/SD(SELECT(Y;SELECTED))

X1_norm= SELECT(X1;SELECTED)/SD(SELECT(X1;SELECTED))

X2_norm= SELECT(X2;SELECTED)/SD(SELECT(X2;SELECTED))

X3_norm= SELECT(X3;SELECTED)/SD(SELECT(X3;SELECTED))

X4_norm= SELECT(X4;SELECTED)/SD(SELECT(X4;SELECTED))

Результат сохраним в новых столбцах.

 

Обновим процедуру корреляционного анализа: посчитаем без учета аномальных наблюдений.

 

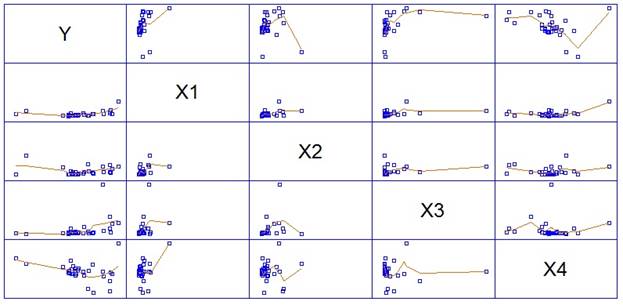
Рис. 2.Графики разброса показателей с линиями локально взвешенной регрессии после исключения аномальных наблюдений

Таблица 2. Корреляционная матрица переменных после исключения аномальных наблюдений

	Y	X1	X2	X3	X4
Y		0,3866	0,0075	0,3966	-0,2800
		(31)	(31)	(31)	(31)
		0,0317	0,9682	0,0272	0,1271
X1	0,3866		0,5004	0,3563	0,4495
	(31)		(31)	(31)	(31)
	0,0317		0,0041	0,0492	0,0112
X2	0,0075	0,5004		0,2838	0,0377
	(31)	(31)		(31)	(31)
	0,9682	0,0041		0,1219	0,8405
X3	0,3966	0,3563	0,2838		0,0117
	(31)	(31)	(31)		(31)
	0,0272	0,0492	0,1219		0,9502
X4	-0,2800	0,4495	0,0377	0,0117
	(31)	(31)	(31)	(31)
	0,1271	0,0112	0,8405	0,9502