Расчет параметров регуляторов внутреннего контура

 

Согласно таблице 3.1 (лекция 3.3) рассчитаем регулятор 1-го типа:

Зададимся в замкнутой системе обобщенным динамическим параметром 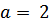. Далее определим коэффициенты усиления регулятора, придающие замкнутой системе заданные качества:

где


Тогда выражение 3.2 примет вид:

Рисунок 3.4. Модель замкнутого внутреннего контура системы с регулятором 1-го типа

 


Динамические характеристики, полученные на этой модели, показаны на рисунках 3.5 и 3.6.

Рисунок 3.5. Реакция замкнутого внутреннего контура системы с регулятором 1-го типа на единичный скачок

Рисунок 3.6. ЛАХ и ЛЧХ замкнутого внутреннего контура системы с регулятором 1-го типа

 


Теперь, для сравнения, рассмотрим регулятор 2-го типа:

где

– постоянная времени.

- коэффициент усиления регулятора, который находится по формуле

Зададим тогда:

Рисунок 3.7. Модель замкнутого внутреннего контура системы с регулятором 2-го типа (TD = 0.1)

Тогда выражение примет вид:

 

 

Динамические характеристики, полученные на этой модели, показаны на рисунках 3.8 и 3.9

Зададимся другим значением , подставляя данные в выражение 3.9, с учётом получим:

В таком случае выражение примет вид:

Рисунок 3.9. ЛАХ и ЛЧХ замкнутого внутреннего контура системы с регулятором 2-го типа (TD = 0.1)

Рисунок 3.8. Реакция замкнутого внутреннего контура системы с регулятором 2-го типа на единичный скачок (TD = 0.1)


Рисунок 3.10. Модель замкнутого внутреннего контура системы с регулятором 2-го типа (TD = 0.01)
Рисунок 3.11. Реакция замкнутого внутреннего контура системы с регулятором 2-го типа на единичный скачок (TD = 0.01)  

Модель для показана на рисунке 3.10, а её динамические характеристики показаны на рисунках 3.11 и 3.12.

 

 

Рисунок 3.12. ЛАХ и ЛЧХ замкнутого внутреннего контура системы с регулятором 2-го типа (TD = 0.01)  

Исходя из полученных результатов, видим, что система с TD = 0.01 более качественная (по времени переходного процесса и перерегулированию), чем система с TD = 0.1. Отличие между системами с разными типами регуляторов не существенно.