Нелинейная множественная регрессия. Производственная функция
Для линейного регрессионного анализа требуется линейность только по параметрам, поскольку нелинейность по объясняющим переменным может быть устранена с помощью метода замены переменных. Например, зависимость: 
может быть переписана в форме, которая будет линейной по объясняющим переменным 
, 
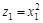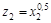следующим образом: 
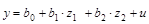. Если случайная составляющая и в начальном уравнении регрессии удовлетворяет предпосылкам нормальной модели, то она будет им удовлетворять и в преобразованном уравнении регрессии.
Нелинейность по параметрам является более серьезной проблемой. Однако если имеет место показательная, либо степенная зависимость и случайная составляющая входит в модель мультипликативно, то модель может быть линеаризована посредством логарифмирования обеих ее частей. Например, функция спроса: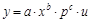 
, где у – объем потребления товара; х – доход; р – цена; и – случайная .составляющая, может быть преобразована в форму, которая является линейной по параметрам:
При этом коэффициент при Lnх будет непосредственной оценкой b – эластичности спроса по доходу, коэффициент при Lnр будет оценкой c – эластичности спроса по цене.
Производственная функция. Производственная функция! представляет собой математическую модель, характеризующую зависимость объема выпускаемой продукции от факторов производства. При этом модель может быть построена как для отдельной фирмы и отрасли, так и для всей национальной экономики. Рассмотрим производственную функцию, включающую два фактора производства: затраты капитала K и трудовые затраты L, определяющие объем выпуска Q, Тогда можно записать: Q=f(K,L).
Определенного уровня выпуска можно достичь с помощью различного сочетания капитальных и трудовых затрат. Кривые, описываемые условиями f(K,L)=const, называют изоквантами. Предполагается, что по мере роста значений одного из факторов предельная норма замещения данного фактора производства уменьшается. Поэтому при сохранении постоянного объема производства экономия (сокращение) одного вида затрат, связанная с увеличением затрат другого фактора, постепенно уменьшается.
Рассмотрим подробно производственную функцию Кобба-Дугласа, которая для двух факторов производства имеет вид: 
, где А, a, b – параметры модели.
Величина А зависит от единиц измерения Q, К, L, атакже от эффективности производственного процесса. При фиксированных значениях К и L функции, характеризующейся большей величиной параметра А, соответствует большее значение Q, следовательно, и производственный процесс, описываемый такой функцией, более эффективен.
Параметры a и b называют коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменится Q, если a и b увеличить соответственно на 1 %. Можно предположить, что обе величины a и b находятся между нулем и единицей. Они должны быть положительными, так как увеличение затрат производственных факторов должно вызвать рост объема выпуска. Скорее, всего, они будут меньше единицы, так как разумно предположить, что рост объема выпуска происходит медленнее, чем рост производственных затрат, если другие факторы остаются постоянными.
Эффект от масштаба производства. Рассмотрим поведение производственной функции при изменении масштабов производства. Предположим для этого, что затраты каждого фактора производства увеличились в С раз. Тогда новое значение будет определяться следующим образом:
.
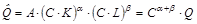Если (a + b) > 1, то говорят, что функция имеет возрастающий эффект от масштабов производства. Это значит, что если К и L увеличиваются в некоторой пропорции (С раз), то Q растет в большей пропорции (Сa+b раз, что больше С).
Если (a + b) =1, то говорят, что функция имеет постоянный эффект от масштабов производства. Это значит, что Q увеличивается в той же пропорции, что и К и L.
Если (a + b) < 1, то говорят, что функция имеет убывающий эффект от масштабов производства. Это значит, что Q увеличивается в меньшей пропорции, чем К и(т. к. Сa+b < С).