Дисперсия и ковариация: их смысл и взаимосвязь,оценочные значения.

Дисперсия Var(x) – средний квадрат разброса возможных значений случайной переменной x относительно ее ожидаемого значения:

 

Var(x)= =E(x-m)^{2 =} (1)

Так что Var(x) – это тоже константа, физическая размерность которой равна квадрату физической размерности значений x.

Положительный квадратный корень из дисперсии 𝜎 = √ Var(x ) именуется средним квадратическим отклонением (СКО). Размерности 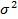и х совпадают. Константа (как: и 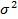) служит характеристикой неопределенности (изменчивости) х. Добавим, что при вычислении Var(х) удобно пользоваться формулой, вытекающей (можно доказать) из предыдущей формулы:

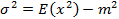(2)

Из формул (1)-(2) видно, что для отыскания величин m, 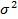нужно знать закон распределения Px(q) случайной переменной х. Часто это закон неизвестен, и тогда можно оценить (приближенно определить) характеристики m, 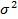по результатам n независимых наблюдений (опытов) над х

 

(х₁,х₂,…,х_т) (3)

В наборе (3) каждая компонента х_i — это случайная переменная с одним и тем же законом распределения Рх(q), при этом величины х_i являются независимыми. Вот формулы для оценивания m и :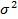

(4)

(5)

С ростом количества наблюдений п точность приближенных формул (4) и (5) возрастает.

 

 

Известно, что ковариация

(6)

Cov(x,y) – числовая характеристика взаимосвязи пары случайных переменных x и y

Дисперсия – частный случай ковариации Cov(x,y)

Из (1) для вычисления ковариации нужно знать закон распределения.

Если он не известен, то Cov можно оценить по выборке из генеральной совокупности XY, xЄX,yЄY{(x_1,y₁₎,(x₂,y₂)…(x_n,y_n)}

X={x,…Xn}

Y={y,…Yn}

Оценкой Cov может служить величина:

(7)

C учетом (8) можно получить:

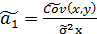(8)

Преобразуем (8) :

=

 

=>

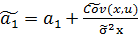
Таким образом, оценка параметра a₁ отличается от своего истинного значения на значение отношения оценки ковариации регрессора и остатка к оценке дисперсии регрессора.

Отсюда видно,что несмотря на то,что случайное возмущение непосредственно не участвует в вычислении значения оценок параметров,они существенно влияют на их качество. А именно: если случайное возмущение коррелируется с регрессором, то значение оценки становится смещенным.