Экспоненциальное приближение
В экспоненциальной модели линия тренда имеет следующее уравнение  . MS Excel выполняет логарифмическое преобразование исходных данных
. MS Excel выполняет логарифмическое преобразование исходных данных 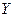 для определения подобранных значений, поэтому значения зависимой переменной должны быть положительными. Если же среди значений
для определения подобранных значений, поэтому значения зависимой переменной должны быть положительными. Если же среди значений 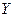 имеются нулевые или отрицательные, то на вкладке Тип окна Линии тренда пиктограмма Экспоненциальная будет выделена серым. Чтобы обойти это ограничение, можно добавить какое-либо число ко всем значениям
имеются нулевые или отрицательные, то на вкладке Тип окна Линии тренда пиктограмма Экспоненциальная будет выделена серым. Чтобы обойти это ограничение, можно добавить какое-либо число ко всем значениям 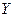 .
.
Данная функция используется для моделирования экспоненциального роста. Пример данных с таким поведением представлен на рис. 2.23.

Рис. 2.23. Данные продаж за год
Временной ряд данных обычно изображают с помощью графика MS Excel, а не точечной диаграммы. Следующие шаги описывают метод построения графика с экспоненциальной линией тренда, показанной на рис. 2.24.
- Введите номера годов и данные продаж, как показано на рис. 2.23.
- Выделите данные о продажах (В2:В9) и щелкните по кнопке Мастера диаграмм.
- На шаге 1 Мастера диаграмм (Тип диаграммы) выберите на вкладке Стандартные «График с маркерами, помечающими точки данных» Нажмите Далее. На шаге 2 (Источник данных диаграммы) на вкладке Ряд щелкните в строке Подписи оси
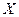 и выберите диапазон А2:А9 листа с помощью перетаскивания. Нажмите Далее. На шаге 3 (Параметры диаграммы) на вкладке Заголовки укажите названия диаграммы и осей, как на рис. 2.24. На вкладке Легенда уберите отметку с пункта Добавить легенду. Нажмите Готово.
и выберите диапазон А2:А9 листа с помощью перетаскивания. Нажмите Далее. На шаге 3 (Параметры диаграммы) на вкладке Заголовки укажите названия диаграммы и осей, как на рис. 2.24. На вкладке Легенда уберите отметку с пункта Добавить легенду. Нажмите Готово. - Щелкните по какой-либо точке данных на диаграмме, чтобы выбрать ряд данных. Щелкните правой кнопкой и выберите Добавить линию тренда в контекстном меню. На вкладке Тип щелкните по пиктограмме Экспоненциальная. На вкладке параметры включите Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности
 . Затем нажмите ОК.
. Затем нажмите ОК.
Так как используется график, а не точечная диаграмма, то MS Excel не использует значение Год в столбце С для приближения экспоненциальной функцией. Данные о годе используются только как метки оси 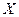 , а роль значений
, а роль значений 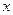 экспоненциальной функции выполняют числа от 1 до 8.
экспоненциальной функции выполняют числа от 1 до 8.

Рис. 2.24. Экспоненциальная линия тренда
Инструмент экспоненциальной линии тренда не находит автоматически значений  и
и  , минимизирующих сумму квадратов отклонений фактических
, минимизирующих сумму квадратов отклонений фактических 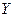 от подобранных (=
от подобранных (=  ). Напротив, MS Excel берет логарифм от обеих частей формулы экспоненциального приближения, что может быть записано так:
). Напротив, MS Excel берет логарифм от обеих частей формулы экспоненциального приближения, что может быть записано так:  и применяет обычную линейную регрессию к значениям зависимой переменной
и применяет обычную линейную регрессию к значениям зависимой переменной  относительно независимой переменной
относительно независимой переменной 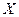 . То есть MS Excel находит наклон и смещение, минимизирующие сумму квадратов отклонений фактических
. То есть MS Excel находит наклон и смещение, минимизирующие сумму квадратов отклонений фактических  от подобранных
от подобранных  , из формулы
, из формулы  . Таким образом, Смещению отвечает
. Таким образом, Смещению отвечает  , а
, а  равно Exp(Смещение). Значение Наклон соответствует
равно Exp(Смещение). Значение Наклон соответствует  в экспоненциальной формуле.
в экспоненциальной формуле.
Следующая последовательность шагов описывает получение более полных характеристик регрессии преобразованных данных в экспоненциальной модели с помощью инструмента анализа Регрессия.
1. Введите данные в столбцы А, В и С, как показано на рис. 2.25. Если данные о Годах и Продажах уже находятся в столбцах А и В, как на рис. 2.23, то выделите столбец В, выберите Добавить Ячейки в контекстном меню, ведите метку Х и целые числа от 1 до 8 в столбец В.
2. Ведите метку Ln(Продажи) в ячейку D1 и формулу =LN(C2) в D2.
3. Скопируйте формулу, выделив D2 и дважды щелкнув по маркеру заполнения в правом нижнем углу. Значения логарифма появятся в столбце D.
4. В меню Сервис выберите Анализ данных. В диалоговом окне Анализа данных выберите Регрессия и нажмите ОК. Появится диалоговое окно Регрессии.
5. Входной интервал 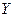 : укажите на листе или введите ссылки на диапазон со значениями зависимой переменной (D1:D9), включая метку в первой строке.
: укажите на листе или введите ссылки на диапазон со значениями зависимой переменной (D1:D9), включая метку в первой строке.
6. Входной интервал 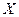 : укажите на листе или введите ссылки на область со значениями независимой переменной (В1:В9), включая метку в первой строке.
: укажите на листе или введите ссылки на область со значениями независимой переменной (В1:В9), включая метку в первой строке.
7. Метки: отметьте эту опцию, так как метки включены во входные интервалы для 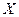 и
и 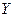 .
.
8. Не выбирайте опции Константа – ноль или Уровень надежности.
9. Параметры вывода: щелкните по кнопке Выходной интервал, выделите строку справа и укажите или введите ссылку на левый верхний угол области шириной в 16 столбцов, куда будут помещены результаты (F1). Можно включить опции для получения Остатков. Затем нажмите ОК.
На рис.2.25 представлены результаты регрессии после удаления части, относящейся к анализу дисперсии. Значения  - квадрат и Стандартной ошибки нельзя прямо сравнивать со значениями, полученными в линейной модели, так как здесь
- квадрат и Стандартной ошибки нельзя прямо сравнивать со значениями, полученными в линейной модели, так как здесь  - квадрат является долей дисперсии
- квадрат является долей дисперсии  , выраженной через
, выраженной через 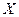 в линейной модели, а Стандартная ошибка выражается в тех же единицах измерения, что и
в линейной модели, а Стандартная ошибка выражается в тех же единицах измерения, что и  .
.

Рис. 2.25. Результаты применения экспоненциальной регрессии
Чтобы определить параметр  формулы в экспоненциальной модели, выделите ячейку G14 и введите формулу =EXP(G12). Для осуществления прогноза средних продаж в экспоненциальной модели введите значение
формулы в экспоненциальной модели, выделите ячейку G14 и введите формулу =EXP(G12). Для осуществления прогноза средних продаж в экспоненциальной модели введите значение 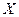 в ячейку (например, 9 в ячейку В10). Затем постройте формулу для предсказанных продаж (поместите =G14*EXP(G13*B10) в ячейку С10).
в ячейку (например, 9 в ячейку В10). Затем постройте формулу для предсказанных продаж (поместите =G14*EXP(G13*B10) в ячейку С10).
Задание. Семь служащих используют одинаковые автомобили для деловых поездок. Водители сообщают среднюю скорость, измеренную в милях в час, и расход топлива в милях на галлон, что приведено в следующей таблице.
| Скорость | |||||||
| Расход топлива |
- Постройте график, линейную и квадратичную линию тренда. Выберите наилучшую линию тренда.
- С помощью инструмента анализа Регрессии определите все характеристики.
- Осуществите прогноз расхода топлива автомобилем, имеющим среднюю скорость 50 миль в час.
Задание. В следующей таблице приведены цены розничной продажи и показатели продаж в долях проданных единиц телевизоров на тысячу посетителей магазина
.
| Цена | $275 | $300 | $325 | $350 | $375 |
| Показатель продаж | 1,60 | 0,95 | 0,65 | 0,50 | 0,45 |
- Постройте график и пять видов трендов в MS Excel. Выберите наилучшую линию тренда.
- С помощью инструмента анализа Регрессии определите все характеристики.
- Осуществите прогноз продаж для магазина, продающего товар по цене $295.