Метод наименьших квадратов. Свойство оценок МНК (формулировка теоремы Гаусса-Маркова)

Метод наименьших квадратов — математический (математико-статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными величинами и др. Состоит в том, что функция, описывающая данное явление, аппроксимируется более простой функцией. Причем последняя подбирается с таким расчетом, чтобы среднеквадратичное отклонение фактических уровней функции в наблюдаемых точках от выровненных было наименьшим.

Рассмотрим механизм применения МНК на примере идентификации модели в виде линейного уравнения парной регрессии:

yt = а₀ + а₁х_t + u_t (2.8)

Для решения задачи имеем набор точек на плоскости или другими словами набор наблюдений за поведением переменных у и л: размером n наблюдений.

y₁ x₁

y₂ х₂ Таблица исходных данных (выборка)

… …

… …

y_n x_n

Согласно методу наименьших квадратов, необходимо найти такие значения оценок параметров модели (2.8), которые соответствуют минимуму суммы квадратов остатков.

Из (2.8) следует, что необходимо найти минимум функции:

Q = ∑_t=1ⁿ (y_t - а₀ - a_lx_t)² (2.9)

Для нахождения параметров функции (2.9), соответствующие ее минимуму, необходимо вычислить производные этой функции по параметрам, приравнять их нулю и решить полученные уравнения относительно а₀ и a₁

2.10

 

Разделив обе части уравнений на «-2» и выполнив перемножения, получим:

∑_t=1ⁿy_t -∑ⁿ_t=1 a₀ – a₁∑ⁿ_t=1x_t =0

∑_t=1ⁿx_ty_t –a₀∑_t=1ⁿx_t –a₁ ∑_t=1ⁿx_t²=0

Или окончательно получаем:

2.11

 

Система уравнений (2.11) называется системой нормальных уравнений для определения оценок параметров модели (2.8).

Убедимся, что решения системы уравнений (2.11) соответствуют минимуму функции (2.9). Для этого достаточно показать, что вторые производные функции (2.9) положительны.

Систему уравнений (2.11) можно решить методом исключения переменных. Для этого достаточно выразить параметр а₀ через а₁( подставить его во второе уравнение системы, откуда легко получить затем полученное значение а х подставить в первое уравнение и получить выражение для а₀ . В результате решение системы уравнений (2.11) примет вид:

2.12

 

Выражения (2.12) позволяют по известным значениям наблюдений за переменными х и j вычислить оценки параметров модели парной регрессии. Проверим, насколько полученные оценки отвечают требованию несмещенности. Для этого запишем второе выражение (2.12) в виде:

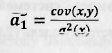2.13

 

Для получения выражения (2.13) необходимо вспомнить, что оценка ковариации и дисперсии случайных переменных вычисляются, как:

2.14

 

Раскрыв скобки и произведя несложные преобразования, легко получить выражение (2.13). Преобразуем (2.13) к виду:

2.15

 

Первое слагаемое в выражении (2.15) равно нулю, т.к. параметр а₀ константа, a cov(x,x)=σ(Х). Тогда окончательно выражение (2.15) принимает вид:

2.16

Математическое ожидание оценки параметра равно правой части выражения (2.16), т.к. параметр и количественные характеристики случайных переменных константы.

Отсюда видно, не смотря на то, что случайные возмущения напрямую не учувствуют в вычислении значений оценок параметров, они существенно влияют на их качество, а именно, если случайное возмущение коррелирует с регрессором, то значение оценки становится смещенным.

Теорема Гаусса-Маркова формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

Теорема начинается с описания условий, которые накладываются на вектор случайных возмущений. Эти условия принято называть предпосылками теоремы Гаусса-Маркова.

И так. Если:

1. Математическое ожидание случайных возмущений во всех наблюдениях равно нулю.

2. Дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе

3. Ковариация между парами случайных возмущений в наблюдениях равны нулю (случайные возмущения в наблюдениях независимы)

4. Ковариация между вектором регрессоров и вектором случайных переменных равна нулю (регрессоры и случайные возмущения независимы)

Тогда. Если матрица X неколлинеарная (нет ни одного столбца, который можно было бы представить в виде линейной комбинации других его столбцов).

1. Наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется, как

2.Ковариационная матрица оценок параметров модели вычисляется, как:

3. Дисперсия случайного возмущения равна:

4.Наилучший прогноз по модели в точке

вычисляется по правилу:

5.Ошибка прогноза эндогенной переменной равна: