Метод наименьших квадратов. Предпосылки применения метода для оценивания регрессионной модели. Система нормальных уравнений и ее решение.

 

Согласно МНК неизвестные параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений 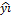, найденных по уравнению регрессии 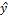= 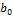+ 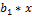, была минимальной: = = ) = )

= [ =

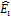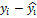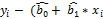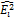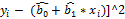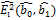
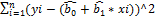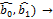S = = = S( min

Функция S зависит от двух переменных b0 и b1 на основании необходимого условия экстремума приравниваем к нулю ее частные производные первого порядка по каждой из переменных:

=

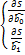= 2 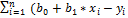)=0

2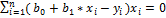

Откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:

 

=

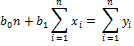
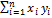
Теперь, разделив обе части уравнения на n, получим систему нормальных уравнений в виде:

=

 

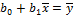
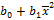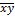
Решением этой системы являются искомые значения коэффициентов выборочной функции регрессии, которые можно рассчитать по формулам:

 

=

 

= - *

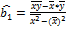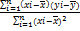
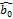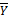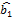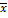
Коэффициент b1 называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по X. Коэффициент регрессии показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной Х на одну единицу.

Таким образом, мы получим выражение выборочной функции парной линейной регрессии, которое является оценкой функции парной линейной регрессии для ГС.

Предпосылки:

1. случайный характер остатков;

2. нулевая средняя величина остатков, не зависящая от xi;

3. гомоскедастичность – дисперсия каждого отклонения ei, одинакова для всех значений x ;

4. отсутствие автокорреляции остатков – значения остатков ei распределены независимо друг от друга;

5. остатки подчиняются нормальному распределению.

Если распределение случайных остатков ei не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

Свойства коэффициентов функции регрессии, полученных с помощью МНК:

Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.

Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки.

Указанные критерии оценок (несмещенность, состоятельность и эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии ei.