Анизотропный гетеропереход

Гетеропереход называется изотипным, если он образован двумя полупроводниками дойками с разными 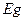, но одинакового типа электропроводности (электронного-n или дырочного-p). Если же эти полупроводники имеют различные типы легирования, то гетеропереход называется анизотипным. Электронные и дырочные типы проводимости для узкозонного полупроводника принято обозначать n и p, а для широкозонного - N и Р, соответственно.

Рассмотрим соприкосновение двух анизотипных полупроводников с раз­ными 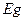, т.е. p-N-гетеропереход.

Также как и в обычном p-n переходе, из требования термодинамического равновесия вытекает условие образования области пространственного заряда (ОПЗ) анизотипного гетероперехода. При отсутствии внешних полей во всем объеме кристалла уровень Ферми должен быть постоянным, т.е. . На языке термодинамики это означает, что все возможные состояния нахождения электронов должны быть равновероятными по всему объему кристалла (второй закон термодинамики).

На границе соединения двух анизотипных полупроводников возникают (после их соприкосновения) градиенты концентраций основных носителей 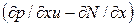, которые приводят к диффузионному переносу основных носителей через гетеропереход и образованию областей ионизированных примесей по обе стороны гетерограницы. Последние, в свою очередь, создают электрическое поле, препятствующее переходу носителей через гетеропереход (дырок в N-область и электронов в p-область).

При достижении условия равенства дрейфового тока, обусловленного растущим электрическим полем ионизированных примесей, и диффузионного тока обусловленного градиентами концентраци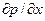и и 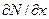возникает равновесное состояние, при котором полный ток носителей становится равным нулю. Уровень Ферми во всем кристалле становится постоянным.

Пространственное распределение электрического потенциала V(x) от расстояния (от координаты x, направленной от p-типа полупроводника к N-типу с началом отсчета в точке соприкосновения двух полупроводников) находится решением уравнения Пуассона:

 

 

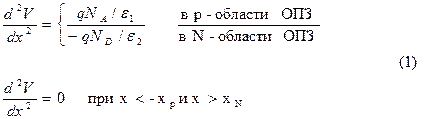
при граничных условиях:

 

 

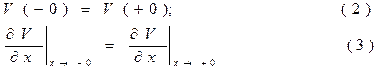
где q - заряд электрона,

и - диэлектрические проницаемости p-области и N-области, знаки ±0, условные, указывающие на N-области и p-области гетероперехода, соответственно.

Решения V(x) для каждой области гетероперехода имеют вид:

 

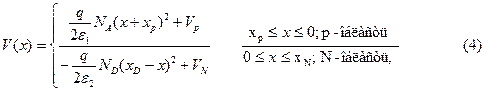
где 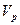и 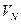постоянные интегрирования уравнения (1), связанные друг с другом условием непрерывности при x = 0 (граничное условие (2))

 

 

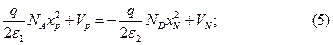
второе граничное условие (3) дает:

 

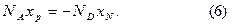
Величину 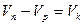называют внутренней разностью потенциалов, диффузионным потенциалом, потенциальным барьером или контактной разностью потенциалов.

Итак, из (5) имеем:

 

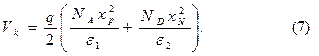
Электрическое поле 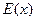, которое равно производной потенциала по координате определяется как:

 

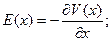
Подстановка из (4) в эту формулу дает:

 

 

Поле достигает максимального значения при x=0:

 

 

Таким образом, электрическое поле растет линейно по абсолютной величине от нуля на границе области пространственного заряда 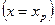в p-области до значения 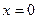, при котором , затем при положительных до 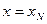электрическое поле падает линейно до нуля.

Из (4) следует, что область гетероперехода, а именно область ионизированных примесей или ОПЗ, простирается от точки в p-области и до точки 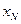в N-области. Полная ширина ОПЗ будет:

 

 

С помощью соотношений (5), (6), (7) и (8) имеем выражение для d:

 

 

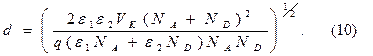
Если к кристаллу с анизотипным гетеропереходом приложено внешнее на­пряжение U, то это выражение принимает вид:

 

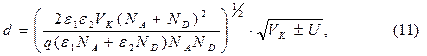
знак "+" соответствует внешнему смещению обратной полярности, что приво­дит к увеличению ОПЗ; знак « - » соответствует прямому внешнему смещению (т.е. когда к р-области приложено внешнее напряжение положительной полярности, а к N-области - отрицательной). В излучателях на полупроводниковом гетеропереходе реализуется послед­ний случай, а именно, к гетеропереходу прикладывается положительное сме­щение. При этом уменьшается толщина ОПЗ, после достижения внешнего напряжения значению порядка контактной разности потенциала , ОПЗ исчезает (d = 0) и через гетеропереход протекает диффузионный ток в прямом направлении.