Пример 3.3

Рассмотрим задачу об использовании сырья (пример 2.1)

Математическая модель данной задачи имеет вид:

F = 3x₁ + 2x₂ ® max,

x₁ + 2x₂ £ 6

2x₁ + x₂ £ 8

- x₁ + x₂ £ 1

x₂ £ 2

x₁, x₂³0

Приведем данную модель к каноническому виду.

1. Целевая функция удовлетворяет требованию максимизации, т.е. соответствует каноническому виду.

2. Система ограничений представляет собой систему неравенств типа «≤». Приводим ее к системе ограничений-равенств путем введения в каждое из неравенств неотрицательной дополнительной переменной с коэффициентом «+1»:

 

x₁ + 2x₂ + x₃ =6,

2x₁ + x₂ +x₄ =8,

-x₁ + x₂ +x₅ =1,

x₂ +x₆ =2.

Дополнительные переменные имеют определенный экономический смысл. Для данной задачи дополнительные переменные х₃ и х₄ отражают расход и наличие производственных ресурсов (т.е. продуктов А и В соответственно), а их числовое значение в плане задачи равно объему неиспользованного соответствующего ресурса; дополнительные переменные х₅ и х₆ характеризуют величину дисбаланса между планируемым объемом производства и величиной спроса.

3. Согласно экономическому содержанию все переменные задачи могут принимать только неотрицательные значения, т.е. x_j³0, .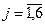

Таким образом, исходная задача приведена к канонической форме. Система ограничений имеет вид:

 

F=3x₁+2x₂®max,

х₁ + 2x₂ + x₃ =6

2x₁ + x₂ + x₄ =8

-x₁ + x₂ +x₅ =1

x₂ +x₆=2

х_j³0, .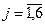

Начальный опорный план данной задачи образуют m=4 единичных вектора: Р₃=(1 0 0 0 ), Р₄=(0 1 0 0 ), Р₅=(0 0 1 0 ), Р₆=(0 0 0 1 ), соответствующие, в данном случае, дополнительным переменным х₃, х₄, х₅, х₆.

Составляем первую симплекс-таблицу.

 

і	Базис	Сб	Р0	3	2	0	0	0	0
Х1	Х2	Х3	Х4	Х5	Х6
	Х3
2	Х4
	Х5			-1
	Х6
5				-3	-2

 

В столбец «Базис» заносим наименование базисных переменных, соответствующих начальному опорному плану.

В столбец «С_б» заносятся коэффициенты при базисных переменных в целевой функции задачи. Так как переменные Х₃, Х₄, Х₅, Х₆ отсутствуют в целевой функции, то их коэффициенты равны нулю.

В столбец «Р₀» заносится столбец свободных членов в системе ограничений.

На пересечении первых 4-х строк и последних 6-ти столбцов, соответствующих переменным задачи, записываем матрицу коэффициентов при неизвестных в системе ограничений.

Элементы индексной строки (5-я строка) заполняются для столбцов Р₀ и Х₁, …, Х₆:

· для столбца Р₀: D₀=С_б*Р₀, т.е. D₀=0*6+0*8+0*1+0*2=0;

· для столбца Х_j, j=1,6 : D_j= С_б*Р_j-с_j

где Р_j – вектор-столбец коэффициентов при переменной Х_j в системе ограничений, с_j – коэффициент при Х_j в целевой функции задачи.

Например, D₁ = 0*1 + 0*2 + 0*(-1) + 0*0 – 3 = -3;

D₂ = 0*2 + 0*1 + 0*1 + 0*1 - 2 = -2.

Для текущих базисных переменных в индексной строке всегда будут стоять нули.

Построенная симплекс-таблица характеризует начальный опорный план задачи: Х₀=(0; 0; 6; 8; 1; 2).

Значения базисных переменных взяты из столбца Р₀, все небазисные переменные, - Х₁ и Х₂, - равны нулю.

Значение целевой функции при данном плане равно: F(x₀)=0 (значение ячейки таблицы D₀).

Этому плану соответствует такая ситуация: ничего не производится, ресурсы не используются, спрос не удовлетворен, а прибыль от реализации равна нулю.

Проверка плана на оптимальность.

Так как D₁ = -3 < 0 и D₂ = -2 < 0, то план Х₀ не оптимальный. Переходим к лучшему плану, выбрав разрешающие столбец и строку.

Разрешающий столбец выбираем из условия:

 

.

 

Таким образом, в новый базис необходимо ввести переменную Х₁ соответствующую D₁.

Для положительных элементов разрешающего столбца рассчитываем:

 

.

 

Данное соотношение определяет разрешающую строку, т.е. ту переменную, которую необходимо вывести из базиса (в нашем случае это Х₄).

Разрешающий элемент a₂₁=2.

Согласно пунктам 4а)-д) алгоритма заполняем новую симплекс-таблицу и проверяем ее на оптимальность.

 

і	Базис	Сб	Р0	3	2	0	0	0	0
Х1	Х2	Х3	Х4	Х5	Х6
1	Х3				3/2		-1/2
	Х1				½		½
	Х5				3/2		½
	Х6
5					-1/2		3/2

 

 

Для переменных нового базиса в соответствующем столбце на пересечении одноименных переменных ставится «1», остальные элементы столбца – «0».

Элементы второй строки новой таблицы (соответствующей разрешающей строке предыдущей таблицы) получаем путем деления элементов разрешающей строки на разрешающий элемент.

Все остальные элементы таблицы пересчитываем по формулам (3.16).

Например элемент 1^й строки столбца Р₀:

 

,

 

или элемент 3-й строки 2-го столбца:

 

и т.д.

 

Таким образом, новый опорный план задачи Х₁ = (4; 0; 2; 0; 5; 2) предусматривает выпуск 4 тонн краски Е (Х₁=4), краска I не выпускается (Х₂=0), продукт В полностью израсходован (Х₄=0), а остаток продукта А – 2 тонны (Х₃=2); дисбаланс между выпуском красок 5 тонн (Х₅=5), а спрос на краску I превышает предложение, т.е. ее выпуск на 2 тонны (Х₆=2).

При таком плане производства фирма получает прибыль, равную F(Х₁)=12 тыс. грн.

Построенный план не оптимален, так как D₂ = ^-1/₂ < 0.

Переходим к лучшему опорному плану, введя в новый базис переменную Х₂ вместо переменной Х₃:

.

Элемент а₁₂ = ³/₂ – разрешающий элемент.

Строим новую симплекс-таблицу согласно пунктам 4а)-д) алгоритма:

 

і	Базис	Сб	Р0	3	2	0	0	0	0
Х1	Х2	Х3	Х4	Х5	Х6
	Х2		4/3				-1/3
	Х1		10/3				2/3
	Х5
	Х6		2/3				1/3
			38/3				4/3

 

В последней симплексной таблице все D_j³0, . Значит, соответствующий ей план является оптимальным, т.е. , .

 

Таким образом, оптимальный план производства предусматривает выпуск ¹⁰/₃ тонн краски Е и ⁴/₃ тонн краски I, прибыль от реализации которой будет максимальной и составит тыс. грн. При данном плане производства продукты А и В полностью израсходованы; дисбаланс между объемом производства красок I и Е составляет 3 тонны/день, а спрос на краску I не удовлетворен на ²/₃ тонны/день.

3.5 Метод искусственного базиса решения задачи линейного программирования

Как показано выше, для задачи, записанной в предпочтительной форме, можно непосредственно указать ее опорный план, т.к. среди векторов Рj, компонентами которых служат коэффициенты при неизвестных в системе уравнений, имеется т единичных. Однако для многих задач линейного программирования, записанных в форме основной задачи и имеющих опорные планы, среди векторов P_j не всегда есть m единичных.

Рассмотрим такую задачу.

Пусть требуется найти максимум функции:

F = c₁x₁ + c₂x₂ + ……+ c_nx_n (3.17)

при условиях:

(3.18)

где b_i ³ 0 ( ), m<.n и среди векторов P₁, P₂, …, P_n нет m единичных.

Задача, состоящая в определении максимального значения функции:

F = c₁x₁ + c₂x₂ + ……+ c_nx_n -Мx_n+1- …- Мx_n+m (3.19)

при условиях:

(3.20)

где M — некоторое достаточно большое положительное число, конкретное значение которого обычно не задается, называется расширенной задачей по отношению к задаче (3.17) - (3.18).

Расширенная задача имеет опорный план: Х=(0; 0; ...; 0; b₁; b₂; ...;b_m), определяемый системой единичных векторов P_n+1; Р_п+2, … Р_п+т, которые образуют базис m-мерного векторного пространства, называемого искусственным. Сами векторы, так же как и переменные x_n+i ( ), называются искусственными. Так как расширенная задача имеет опорный план, то ее решение может быть найдено симплексным методом.

Теорема 3.5 Если в оптимальном плане X*=(x*₁, x*₂, ...; x*_n, x*_n+1; ...; x*_n+m) расширенной задачи (3.19) - (3.20) значения искусственных переменных x*_n+i=0 ( ), то X*=(x*₁, x*₂, ...; x*_n) является оптимальным планом задачи (3.17) - (3.18).

Таким образом, если в найденном оптимальном плане расширенной задачи, значения искусственных переменных равны нулю, то тем самым получен оптимальный план исходной задачи.

Примечание. Расширенная задача решается с помощью описанного в п.3.4 алгоритма табличного симплекс-метода. На практике для удобства его использования в расширенной задаче конкретизируют коэффициенты М при искусственных переменных x_n+i ( ) в целевой функции задачи, присваивая им значения, на порядок превышающие значение любого из коэффициентов при остальных переменных в целевой функции задачи. После чего такая задача решается с помощью обычных симплексных преобразований.

Итерационный процесс ведут до тех пор, пока:

1) либо все искусственные векторы не будут исключены из базиса;

2) либо не все искусственные векторы исключены, но индексная строка не содержит больше отрицательных элементов среди оценок оптимальности ∆₁, …, ∆_n.

В первом случае базис отвечает некоторому опорному плану исходной задачи и определение ее оптимального плана продолжают по общим правилам симплексного метода. Во втором случае исходная задача не имеет решения.

Этапы нахождения решения ЗЛП методом искусственного базиса:

1. Составляют расширенную задачу (3.19) - (3.20).

2. Находят опорный план расширенной задачи.

3. С помощью обычных вычислений симплекс-метода исключают искусственные переменные из базиса. В результате либо находят опорный план исходной задачи (3.17) — (3.18), либо устанавливают ее неразрешимость.

4. Используя найденный опорный план задачи (3.17) — (3.18), либо находят симплекс-методом оптимальный план исходной задачи, либо устанавливают ее неразрешимость.

Рассмотрим пример решения ЗЛП методом искусственного базиса для задачи, математическая модель которой была построена в разделе 2 (пример 2.6).

Пример 3.4 Задача о распределении руды

Математическая модель задачи имеет вид:

Запишем данную задачу в канонической форме:

В системе уравнений последней задачи рассмотрим векторы из коэффициентов при неизвестных:

Среди векторов P₁, Р₂, … P₅ нет единичных. Поэтому в левую часть каждого уравнения системы ограничений задачи вводим искусственные неотрицательные переменные х₆ - х₈ и рассмотрим расширенную задачу:

Расширенная задача имеет опорный план Х=(0; 0; 0; 0; 0; 10; 4; 4), определяемый системой трех единичных векторов: P₆, P₇, Р₈:

.

Для решения расширенной задачи с помощью симплексного метода примем значение М=100. Тогда окончательно получаем ЗЛП, пригодную для применения алгоритма симплексного метода:

Решение оформим последовательностью симплекс-таблиц:

Базис	Сб	Р0	-5	-6	-1			-100	-100	-100
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8
Х6	-100
Х7	-100		0,4	0,6	0,2	-1
Х8	-100		0,6	0,5	0,2		-1
		-1800	-195	-204	-139
Х1=(0; 0; 0; 0; 0; 10; 4; 4), - не оптимальный, F1(Х1)=-1800.
Базис	Сб	Р0	-5	-6	-1			-100	-100	-100
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8
Х6	-100	3,333	0,33		0,7	1,67			-1,7
Х2	-6	6,667	0,67		0,3	-1,7			1,67
Х8	-100	0,667	0,27			0,8	-1		-0,8
		-440	-59		-71	-240
Х2=(0; 6,667; 0; 0; 0; 3,333; 0; 0,667), - не оптимальный, F1(Х2)=-440.

 

Базис	Сб	Р0	-5	-6	-1			-100	-100	-100
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8
Х6	-100		-0,2		0,6					-2
Х2	-6		1,2		0,4		-2
Х4		0,8	0,32				-1,2		-1	1,2
		-248	17,8		-61		-188
Х3=(0; 8; 0; 0,8; 0; 2; 0; 0), - не оптимальный, F1(Х3)=-248.
Базис	Сб	Р0	-5	-6	-1			-100	-100	-100
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8
Х5			-0,1		0,3			0,5		-1
Х2	-6
Х4			0,2		0,4			0,6	-1
		-60	-1		-5
Х4=(0; 10; 0; 2; 1; 0; 0; 0), - не оптимальный, F1(Х4)=-60.
Базис	Сб	Р0	-5	-6	-1			-100	-100	-100
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8
Х3	-1	3,333	-0,3				3,3	1,7		-3,3
Х2	-6	6,667	1,33				-3,3	-0,7		3,3
Х4		0,667	0,33				-1,3	-0,1	-1	1,3
		-43,3	-2,7
Х4=(0; 6,667; 3,333; 0,667; 0; 0; 0; 0), - не оптимальный, F1(Х4)=-43,3.
Базис	Сб	Р0	-5	-6	-1			-100	-100	-100
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8
Х3	-1							1,6	-1	-2
Х2	-6					-4		-0,4		-2
Х1	-5						-4	-0,2	-3
		-38
Х5=(2; 4; 4; 0; 0; 0; 0; 0), - оптимальный, F1(Х5)=-38.

Так как в последней симплексной таблице среди чисел ∆_i ( ) нет отрицательных, то план Х₅ является оптимальным, поскольку все искусственные переменные в нем х₆ - х₈ равны нулю.

Таким образом, Х^*=(2; 4; 4; 0; 0), F_min(Х^*)=-F_1mах(Х^*)=38.

Ответ: оптимальным считается переработка руды в количестве 2, 4 и 4 тонн соответственно по 1-му, 2-му и 3-му процессам. При этом суммарные затраты будут минимальными и составят 38 тыс. грн.

3.6 Двойственность в линейном программировании и ее применение в экономическом анализе