Задача об использовании мощностей (задача о загрузке оборудования)

 

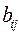Предприятию задан план производства продукции по времени и номенклатуре: требуется за время T выпустить п₁, п₂,..., п_k единиц продукции Р₁, P₂, ...., P_k. Продукция производится на станках S₁, S₂, ..., S_m. Для каждого станка известны производительность (т.е. число единиц продукции P_j, которое можно произвести на станке S_i за единицу времени) и затраты на изготовление продукции P_j на станке S_i в единицу времени.

Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.

Составим экономико-математическую модель задачи.

Обозначим — время, в течение которого станок S_i будет занят изготовлением продукции P_j(i= 1, 2,..., m; j= 1, 2, ..., k).

Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства:

 

Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства:

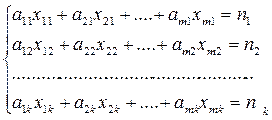Кроме того, на переменные модели, исходя из естественных соображений, накладываются условия неотрицательности:

.

Затраты на производство всей продукции выразятся функцией:

.

Экономико-математическая модель задачи об использовании мощностей примет вид: найти такое решение Х=( ), удовлетворяющее системе ограничений, при котором функция F принимает минимальное значение, т.е.: