Возможные средние дневные затраты фирмы А
| Дневные затраты фирмы A | ||||||
| Ситуация | Стоимость сырья | Убытки от простоя | Транспортные затраты | Затраты на командировку | Затраты на ненормированную работу | Всего в день |
| А1-В1 | ||||||
| А1-В2 | ||||||
| А2-В1 | ||||||
| А2-В2 | ||||||
| А3-В1 | ||||||
| А3-В2 | ||||||
| А4-В1 | ||||||
| А4-В2 |
На пересечении і-ой строки j-го столбика становится платеж второго игрока первому в ситуации, если применяется i-тая стратегия первым игроком и j-тая стратегия вторым. Если выиграет второй игрок, то платеж будет иметь знак минус.
Платежная матрица в задаче (игре), которая рассматривается, имеет размерность 4 х2 и приведена в табл. 4.2. Все платежи имеют отрицательный знак, поскольку определяют в этой задаче затраты фирмы А.
Таблица 4.2
| Стратегии фирмы А | Стратегии фирмы В | |
| В1 | B2 | |
| А1 | -100 | -400 |
| А2 | -150 | -300 |
| А3 | -190 | -250 |
| А4 | -330 | -200 |
Платежная матрица А имеет вид
 -100 -400
-100 -400
-150 -300
-190 -250
-330 -200
Задача фирмы А - найти оптимальную стратегию, которая обеспечивает минимум ожидаемых убытков в условиях неопределенности поведения поставщика (фирма В).
Выбор стратегии поведения фирмы А в условиях, описанных в табл. 4.2, зависит от надежности поставщика, которая выражается количественно в сроках вероятности. Пусть, например, она равняется 40% (это означает, что своевременная поставка имеет место с вероятностью 0,4). Тогда ожидаемые убытки (отрицательный выигрыш) фирмы А при применении первой чистой стратегии А1 составляют
S1(0,4) = -100х0,4-400х0,6 = -280 у.е.,
а при применении четвертой –
S4(0,4) = -330х0,4-200х0,6 = -252 у.е.
Видим, что затраты уменьшились. Если рассчитать убытки при применении других стратегий, то оптимальной будет стратегия А3. В самом деле, применяя вторую стратегию, фирма А будет нести убытки
S2(0,4) = -150х0,4-300х0,6 = -240 у.е.,
а если использует третью стратегию, - только
S3(0,4) = -190х0,4-250х0,6 = -226 у.е.
Управление производственными процессами осуществляется путем реализации последовательности решений. Из-за отсутствия довольно полной информации о состоянии объекта управления возникает неопределенность в принятии решений. Причины этого могут быть разными: невозможность получения информации к моменту принятия решения; очень высокие затраты на получение информации; невозможность устранения неопределенности через объективный характер. Например, случайный характер спроса на продукцию делает невозможным точное прогнозирование объема ее выпуска.
С целью уменьшения неблагоприятных последствий в каждом конкретном случае необходимо учитывать степень риска и существующую информацию. В этом случае человек, который принимает решение, вступает в игровые отношения с некоторым абстрактным лицом, которое условно может назвать "природа". Другими словами, человек, который принимает решение, должен уметь находить управленческое решение, когда природа не выбирает сознательно своих оптимальных стратегий. Любую хозяйственную деятельность можно рассматривать как игру с природой, о состояниях которой иногда известны некоторые вероятности характеристики.
Равнодушие природы к игре (выигрышу) и возможность получения лицом, которое принимает решение, дополнительной информации про ее состояние, отличают игру с природой от обычной матричной игры, в которой принимают участие два сознательных игрока.
Статистические игры являются основной моделью теории принятия решений в условиях частичной неопределенности.
Возвратимся снова к задаче - игры с фирмами А и В. Поскольку такая игра, как правило, не является антагонистической, ее решение нельзя считать оптимальным. В самом деле, фирма-поставщик В не стремится нанести фирме А максимального убытка и поэтому ее надежность может быть любой, необязательно наиболее плохой с точки зрения фирмы А (наиболее плохая для фирмы А - надежность поставщика 0,263).
Если, например, надежность фирмы ВХ1 = 0,4, а фирма А продолжает применять оптимальную для антагонистической игры смешанную стратегию, то ожидаемые затраты фирмы А не снижаются. В самом деле,
S(0,4) = 0,685хS3(0,4) + 0,3S4(0,4) = 0,685(60x0,4-250) + 0,315(-130x0,4-200) = -234,2 у.е.,
где S3 (Х1), S4 (X1) определяются соотношениями (4.3), (4.4).
Чтобы уменьшить затраты для такой надежности поставщика, необходимо отказаться от оптимальной стратегии и использовать, чистую третью стратегию А3 (см. рис, 4.1). Затраты при этом уменьшаются к -226 у.е.
Таким образом, особенностью решения игр с природой в условиях определенности является то, что смешанная стратегия природы задана, то есть известны все вероятности состояний:
Xj, j=1,2,...,n; 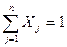 .
.
Это дает возможность для любой j-й чистой стратегии активного игрока вычислить математическое ожидание его выигрыша против известной смешанной стратегии природы по формуле:
 ,
,
где aij — элемент платежной матрицы, расположенный на пересечении i-й строки и j-го столбика:

Максимальный элемент в рассчитанном столбике St (і = 1,m) математических ожиданий выигрышей,
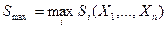 ,
,
определяет наивыгоднейшую стратегию активного игрока и количественно равняется максимально возможному выигрышу. Если максимальных элементов в этом столбике два или больше, то могут использоваться соответствующие им стратегии как в чистом виде, так и в любой комбинации. Такой подход к решению игр против природы имеет место только в том случае, когда вероятности состояний природы заданы. Часто приходится принимать решение при условиях отсутствия информации о таких вероятностях. Тогда, зная возможный перечень состояний природы, считают их равновероятными. При этом для выбора оптимальной стратегии можно использовать критерий максимума математического ожидания выигрыша (критерий Лапласа), но этот критерий может применяться только для равномерного распределения вероятностей Xi = 1/n (і = 1,2,...,n). Рассмотрим другие критерии, которые применяются для решения игр с природой в условиях неопределенности.