Лабораторная работа №13: Решение задач динамического программирования средствами Microsoft Excel и MathCAD.
Цель работы:
Научиться решать задачи динамического программирования используя встроенные возможности MS Excel.
Рекомендации по решению:
1. При решении данных задач динамического программирования средствами Microsoft Excel используются математические функции, которые позволяют найти оптимальные решения.
2. Использование MathCAD требует умения писать программы с использованием встроенного языка программирования.
Задания к лабораторной работе:
| t | ||||||
| R(t) | ||||||
| Z(t) | ||||||
| Смена |
Варианты заданий:
задачи №12.4-12.15 из учебника Исследование операций в экономике / под ред. проф. Кремера. – М.: ЮНИТИ, 2002.
| t_k+1 | U_k+1 | t_k | k =5 | k =4 | ||||
| F_5(t_5) | max F_5 | U_5 | F_4(t_4) | max F_4 | U_4 | |||
| 80-20-40=20 | 80-20-40+50=70 | |||||||
| 75-25=50 | 75-25+35=85 | |||||||
| 65-30=35 | 65-30+25=60 | |||||||
| 60-35=25 | 60-35+20=45 | |||||||
| 60-45=15 |
| k =3 | k =2 | k =1 | ||||||
| F_3(t_3) | max F_3 | U_3 | F_2(t_2) | max F_2 | U_2 | F_1(t_1) | max F_1 | U_1 |
| 80-20-40+85=105 | 80-20-40+120=140 | 80-20+155=215 | ||||||
| 75-25+70=120 | 75-25+105=155 | |||||||
| 80-20-40+85=105 |
В вариантах 1, 2 найти оптимальное распределение средств между n предприятиями при условии, что прибыль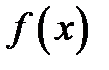 
, полученная от каждого предприятия, является функцией от вложенных в него средств х. Вложения кратны 
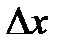, а функция 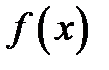заданы таблично.
Вариант 1.
| х | |||||||||
| |||||||||
| |||||||||
|
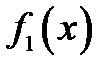
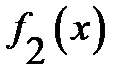
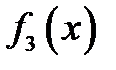
S0=9, n = 3, 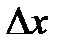=1
Вариант 2.
| х | |||||
|
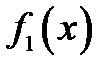
| 0,2 | 0,9 | 1,0 | 1,2 | 2,0 |
|
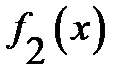
| 1,0 | 1,1 | 1,3 | 1,4 | 1,8 |
|
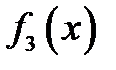
| 2,1 | 2,5 | 2,9 | 3,9 | 4,9 |
| 2,0 | 2,5 | 3,0 | 4,0 |
S0=5, n = 4, 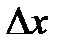=1
Вариант 3.
В условиях задачи (см. Вариант 1) найти оптимальное распределение средств S0=8.
Вариант 4.
В условиях задачи (см. Вариант 1) найти оптимальное распределение средств S0=9, если функция прибыли для четвертого предприятия задана следующей таблицей:
| х | |||||||||
|
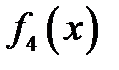
Вариант 5.
В условиях задачи (см. Вариант 1) найти оптимальное распределение средств S0=6 между четырьмя предприятиями.
В вариантах 6-7 найти оптимальное распределение ресурсов S0 между двумя отраслями производства I и II в течение n лет, если даны функции доходов 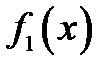и 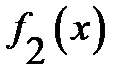для каждой отрасли, функции возврата 
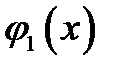и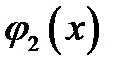 
. По истечении года только все возвращенные средства перераспределяются, доход в производство не вкладывается.
Вариант 6.
S0=40000 ед.; n =4; 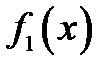= 0,4х; 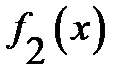= 0,3х; 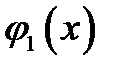= 0,5х; 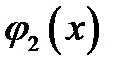= 0,8х.
Вариант 7.
S0=10000 ед.; n =4; 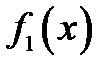= 0,1х2; 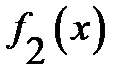= 0,5х; 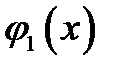= 0,75х; 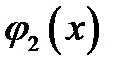= 0,3х.
В вариантах 8-10 составить математическую модель, записать уравнения Беллмана и решить графически следующие задачи на определение оптимальных сроков замены оборудования. Даны: первоначальная стоимость оборудования p0, стоимость содержания r (t) в течение года оборудования возраста t лет, n – срок эксплуатации, в конце которого оборудование продается. Критерий оптимальности – суммарные затраты на эксплуатацию оборудования в течение n лет с учетом первоначальной покупки и последующей продажи.
Вариант 8.
p0=8000;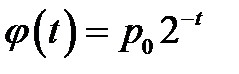 
; 
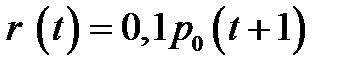; n =5.
Вариант 9.
n =5. Стоимость нового оборудования зависит от года покупки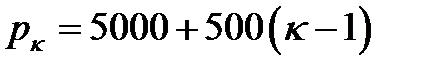 
, 
; 
; 
.
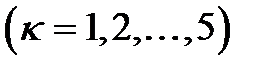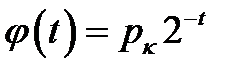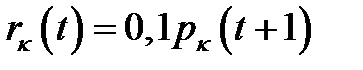Вариант 10.
p0=8000; n =5;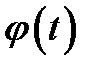 
и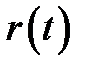 
заданы таблично:
| t | ||||||
|
| – | |||||
|
| – |
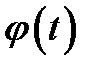
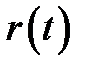
Вариант 11.
Вариант 12.