Карты Карно
Карта Карно для n переменных – это таблица, в которой 
клеток. Число строк и столбцов таблицы – это степени двойки. Каждая клетка соответствует одной из конституент единицы (нуля), т.е. одному из наборов значений переменных. Наборы расположены в карте Карно так, что соседние конституенты можно склеить. Именно, соседними считаются конституенты, расположенные в монолитных областях.
Монолитная область– это множество клеток, образующих строку, столбец, прямоугольник или квадрат, причем число строк и столбцов всякой монолитной области – это степень двойки. В частности, 
. Строки (столбцы), лежащие на границах карты также является соседними.
Приведем эталонные карты Карно для трех и четырех переменных. В клетках запишем наборы значений переменных, и конституенты единицы (нуля), эти клеткам соответствующие.
Эталонная карта Карно для функции трех переменных, ДНФ(табл. 4)
Таблица 4
|
| 
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
Эталонная карта Карно для функции трех переменных, КНФ(табл. 5)
Таблица 5
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эталонная карта Карно для функции четырех переменных, ДНФ(табл. 6)
Таблица 6
|
|
|
| 
| ||
|
|   1100
| 
 1110
|
0110
| 
| |
|
|   1101
|
1111
|
0111
|  0101
| 
|
|
| 1001
|
1011
|
0011
| 0001
|
|
| 
 1000
| 1010
| 0010
|
| |
|
|
|
|
Примеры монолитных областей.
1. 
2. 
3. 
.
Если на карте Карно закрасить монолитные области, результирующая импликанта легко выписывается.
Так, если закрасить монолитную область 2, становится видно, что после склейки в импликанте исчезнут переменные 
, а останется произведение 
.
Эталонная карта Карно для функции четырех переменных, КНФ(табл. 7)
Таблица 7
|
|
|
|
| ||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
|
|
|
Построим карты Карно для нашей функции и определим по ним ее минимальные ДНФ и КНФ. В карте для ДНФ в клетках, соответствующих наборам, на которых функция равна 1, запишем единицы (табл. 8). В карте для КНФ в клетках, соответствующих наборам, на которых функция равна нулю, запишем нули (табл. 9). Чтобы построить минимальную ДНФ (КНФ) нужно «накрыть» клетки с единицами (нулями) минимальным числом монолитных областей максимальной площади и выписать импликанты, соответствующие выбранным монолитным областям.
Минимизация ДНФ
Таблица 8
|
|
|
|
| ||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
|
|
|
Минимизация КНФ
Таблица 9
|
|
|
|
| ||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
|
|
|
|
На карте Карно для ДНФ имеются пять монолитных областей: одна состоит из четырех клеток, четыре из двух. Этим областям соответствуют такие импликанты единицы: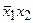 
; 
; 
: 
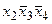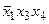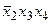; . Чтобы “накрыть” все 8 единиц достаточно четырех монолитных областей, причем сделать это можно двумя способами, поэтому получаются две минимальные ДНФ нашей функции:
На карте Карно для КНФ также выделяются пять монолитных областей. Одна из них содержит 4 клетки, остальные - по две. Этим областям соответствуют такие импликанты нуля: 
; 
; 
; 
; 
. Чтобы “накрыть” все 8 нулей достаточно использовать 4 монолитные области, причем возможны 2 варианта выбора этих областей из 5 имеющихся. Всего, таким образом, строятся две минимальные КНФ данной функции:
Опубликованный материал нарушает авторские права?.