Вторая итерация
Шаг 2. Определим соответствие Г(р) и обновим временные пометки вершин, входящих в это соответствие.
Г(p) = Г(X5) = {X2, X3, X5, X6}
Так как вершина X5 имеет постоянную пометку, то ее не рассматриваем.
l(X2) = min{l(X2); l(p) + c(p(X2))} = min {7, 5+12} = 7
l(X3) = min{l(X3); l(p) + c(p(X3))} = min {∞, 5+11} = 16
l(X6) = min{l(X6); l(p) + c(p(X6))} = min {8, 5+10} = 8
Шаг 3. Выберем минимальную пометку из всех временных, сделаем ее постоянной и присвоим «р» номер, соответствующий этой вершине
min{7, 16, 10, 8} =7 соответствует X2 => l(X2*)= 7+
p= X2
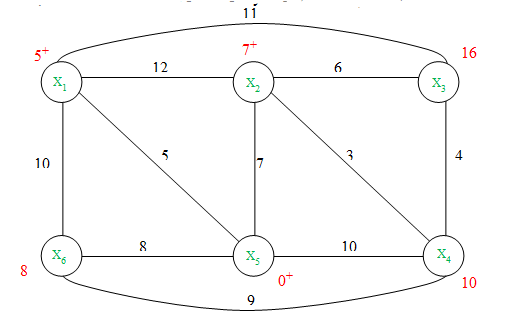
Так как не все вершины имеют постоянные пометки, то переходим к следующей итерации