Алгоритм декодирования Витерби.

Рекуррентный характер процесса сверточного кодирования открывает путь к также рекуррентному и эффективному с вычислительной точки зрения алгоритму декодирования, получившему наименование алгоритма Витерби (по имени автора, предложившего в 1967 г. данный способ декодирования). Сразу же следует подчеркнуть, что алгоритм Витерби является оптимальным, т.е. максимально правдоподобным, и заключается в нахождении кодового слова, наиболее близкого к принятому наблюдению. Первоначально рассмотрим его применение для случая жестких решений, т.е. для двоичного симметричного канала, когда наблюдение 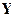декодируется в такое кодовое слово, которое находится на наименьшем расстоянии Хэмминга относительно принятого 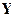. Основная идея декодирования по Витерби заключается в поэтапном сравнении всех путей решетчатой диаграммы (которые в точности представляют собой кодовые слова) с наблюдением 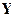и отбрасывании тех из них, которые находятся на большем расстоянии от 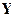, чем некоторые другие. Если два пути, входящих в один и тот же узел, характеризуются различными расстояниями от наблюдения до данного узла, то у пути, обладающим большим расстоянием, отсутствует возможность стать впоследствии более близким к наблюдению, оставаясь на большем расстоянии при любом общем продолжении обоих путей. Следовательно, из двух входящих в узел путей более удаленный от наблюдения может быть исключен из поиска ближайшего пути. Более подробно процедура декодирования может быть описана следующим образом.

Назовем 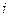–м шагом (этапом) декодирования временной интервал, в течение которого принимается 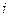–я –символьная кодовая группа (кадр) наблюдения 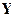. Как раз перед этим моментом рассматриваемые пути (т.е. кодовые слова) могут проходить через один из узлов (состояний) решетчатой диаграммы. На 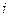–м шаге:

1. Определяются хэмминговы расстояния между принятой –символьной кодовой группой и каждой из ветвей решетчатой диаграммы. Поскольку из каждого из узлов (состояний) выходят две ветви, всего вычисляется расстояний.

2. Рассматриваются две ветви, идущие из разных предшествующих состояний к каждому из узлов:

2.1. Отвечающие указанным ветвям расстояния Хэмминга прибавляются к накопленным до 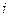–го шага расстояниям Хэмминга двух соответствующих путей для получения новых значений расстояний. Указанное накапливаемое расстояние пути называется метрикой.

2.2. Сравниваются метрики двух соревнующихся путей, идущих в одно и то же состояние. Путь, находящийся на большем расстоянии от наблюдения, чем другой, отбрасывается и больше не учитывается в процедуре декодирования. Оставшийся путь называется выжившим путем.

3. Для всех выживших путей запоминаются значения их метрик и декодер готов к переходу на 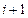–й шаг процедуры.

На основании рассмотренных операций становится ясным, что ресурсосбережение алгоритма заключается в отбрасывании на каждом шаге ровно половины из возможных путей, ведущих в узлов решетки. В результате число выживших путей остается постоянным и равным различных состояний вне зависимости от величины соревнующихся кодовых слов, число которых удваивается на каждом шаге алгоритма декодирования. Для лучшего понимания алгоритма Витерби рассмотрим в подробностях его функционирование на конкретном примере.