Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM1|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.
Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

В этом и состоит геометрический смысл дифференциала.
ифференциал функции обладает свойствами, аналогичными свойствам производной.
1. Дифференциал постоянной равен нулю:
dc = 0, с = const.
2. Дифференциал суммы дифференцируемых функцийравен сумме дифференциалов слагаемых:
d(u+v)=du + dv
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
d(u+c) = du (c= const).
3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
d(uv) = udv + vdu.
Следствие. Постоянный множитель можно выносить за знак дифференциала
d(cu) = cdu (с = const).
4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой

5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Инвариантность дифференциала
Пусть, как в предыдущем параграфе,  -- сложная функция, в которой
-- сложная функция, в которой  -- промежуточные переменные. Найдём и сравним друг с другом дифференциалы функций
-- промежуточные переменные. Найдём и сравним друг с другом дифференциалы функций  и
и  , то есть дифференциалы величины
, то есть дифференциалы величины  , вычисленные:
, вычисленные:
а) в предположении, что независимыми переменными служат  ;
;
б) в предположении, что независимыми переменными служат  .
.
В случае а) дифференциал равен

В случае б) дифференциал, с учётом формулы для производной сложной функции, можно вычислить так:

| |

| |

|
Полученное выражение совпадает по виду с тем, что получено для  в п. а). Разница лишь в том, что вместо дифференциалов независимых переменных
в п. а). Разница лишь в том, что вместо дифференциалов независимых переменных  теперь стоят дифференциалы функций
теперь стоят дифференциалы функций  . Это свойство называетсяинвариантностью дифференциала. Оно свидетельствует о том, что формулу
. Это свойство называетсяинвариантностью дифференциала. Оно свидетельствует о том, что формулу

можно применять, не заботясь о том, являются ли  независимыми или же промежуточными переменными.
независимыми или же промежуточными переменными.
Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

Производные более высокого порядка (если они существуют), определяются как

Для нахождения производных высшего порядка можно использовать следующие формулы:

В частности, для производной второго и третьего порядка формула Лейбница принимает вид

Гладкая функция или непрерывно дифференцируемая функция — это функция, имеющая непрерывную производную на всём множестве определения.
[править]Основные сведения
Рассматривают также гладкие функции высших порядков, а именно, функция с порядком гладкости  имеет непрерывную производную порядка
имеет непрерывную производную порядка  . Множество таких функций, определённых в области
. Множество таких функций, определённых в области  обозначается
обозначается  .
.  означает, что
означает, что  для любого
для любого  , а
, а  означает, что
означает, что 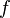 — аналитическая.
— аналитическая.
Например,  - множество непрерывных на
- множество непрерывных на  функций, а
функций, а  - множество непрерывно-дифференцируемых на
- множество непрерывно-дифференцируемых на  функций, т.е. функций имеющих в каждой точке этой области непрерывную производную.
функций, т.е. функций имеющих в каждой точке этой области непрерывную производную.
Если порядок гладкости не указан, то обычно предполагают его достаточным для того, чтобы имели смысл все действия, выполняемые над функцией по ходу текущего рассуждения.
Для тонкого анализа классов дифференцируемых функций вводят также понятие дробной гладкости в точке или показателя Гёльдера, которое обобщает все выше перечисленные понятия гладкости.
Функция 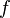 принадлежит классу
принадлежит классу  , где
, где  — целое неотрицательное число и
— целое неотрицательное число и  , если имеет производные до порядка
, если имеет производные до порядка  включительно и
включительно и  является гёльдеровской с показателем
является гёльдеровской с показателем  .
.
В переводной литературе, наравне с термином «показатель Гёльдера», используется термин «показатель Липшица».
Дифференциалом порядка n, где n > 1 от функции  в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть
в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть
 .
.
| Содержание [убрать] · 1 Дифференциал высшего порядка функции одной переменной · 2 Дифференциал высшего порядка функции нескольких переменных · 3 Неинвариантность дифференциалов высшего порядка · 4 Дополнения · 5 Литература |
[править]Дифференциал высшего порядка функции одной переменной
Для функции, зависящей от одной переменной  второй и третий дифференциалы выглядят так:
второй и третий дифференциалы выглядят так:


Отсюда можно вывести общий вид дифференциала n-го порядка от функции  :
:

При вычислении дифференциалов высших порядков очень важно, что  есть произвольное и не зависящее от
есть произвольное и не зависящее от  , которое при дифференцировании по
, которое при дифференцировании по  следует рассматривать как постоянный множитель.
следует рассматривать как постоянный множитель.
[править]Дифференциал высшего порядка функции нескольких переменных
Если функция  имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:
имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .
.




Символически общий вид дифференциала n-го порядка от функции  выглядит следующим образом:
выглядит следующим образом:

где  , а
, а  произвольные приращения независимых переменных
произвольные приращения независимых переменных  .
.
Приращения  рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.
рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.
Неинвариантность дифференциалов высшего порядка
При  ,
,  -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение
-й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение  зависит, вообще говоря, от того, рассматривается ли переменная
зависит, вообще говоря, от того, рассматривается ли переменная  как независимая, либо как некоторая промежуточная функция другого переменного, например,
как независимая, либо как некоторая промежуточная функция другого переменного, например,  .
.
Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
При n = 2 и  :
:
· если  — независимая переменная, то
— независимая переменная, то 
· если  и
и 
1. 
2. при этом,  и
и 
С учётом зависимости  , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.
, уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
| Содержание [убрать] · 1 Определение · 2 Связанные определения · 3 Свойства o 3.1 Формула Тейлора o 3.2 Различные формы остаточного члена · 4 Ряды Маклорена некоторых функций · 5 Формула Тейлора для функции двух переменных · 6 См. также · 7 Литература |
[править]Определение
Пусть функция  бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд
. Формальный ряд

называется рядом Тейлора функции 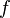 в точке
в точке  .
.
[править]Связанные определения
· В случае, если  , этот ряд также называется рядом Макло́рена.
, этот ряд также называется рядом Макло́рена.
[править]Свойства
· Если 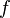 есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке
есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке  области определения
области определения 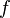 сходится к
сходится к 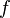 в некоторой окрестности
в некоторой окрестности  .
.
· Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности  . Например, Коши предложил такой пример:
. Например, Коши предложил такой пример:

У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке  равны нулю.
равны нулю.
[править]Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
· Пусть функция  имеет имеет  производную в некоторой окрестности точки производную в некоторой окрестности точки  , ,  · Пусть
· Пусть  · Пусть
· Пусть  — произвольное положительное число,
тогда: — произвольное положительное число,
тогда: 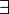 точка точка  при при  или или  при при  : :

|
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
[править]Различные формы остаточного члена
В форме Лагранжа:

В форме Коши:

В интегральной форме:

Ослабим предположения:
· Пусть функция  имеет
имеет  производную в некоторой окрестности точки
производную в некоторой окрестности точки 
· И  производную в самой точке
производную в самой точке  , тогда:
, тогда:
 — остаточный член в асимптотической форме (в форме Пеано, в локальной форме)
— остаточный член в асимптотической форме (в форме Пеано, в локальной форме)
[править]Ряды Маклорена некоторых функций
· Экспонента: 
· Натуральный логарифм:  для всех
для всех 
· Биномиальное разложение:  для всех
для всех  и всех комплексных
и всех комплексных  где
где 
· Квадратный корень:  для всех
для всех 
·  для всех
для всех 
· Конечный геометрический ряд:  для всех
для всех 
· Тригонометрические функции:
· Синус: 
· Косинус: 
· Тангенс:  для всех
для всех  где
где  — Числа Бернулли
— Числа Бернулли
· Секанс:  для всех
для всех  где
где  — Числа Бернулли
— Числа Бернулли
· Арксинус:  для всех
для всех 
· Арктангенс:  для всех
для всех 
· Гиперболические функции:
· 
· 
·  для всех
для всех 
·  для всех
для всех 
·  для всех
для всех 
[править]Формула Тейлора для функции двух переменных
Пусть функция  имеет полные производные вплоть до
имеет полные производные вплоть до  -го порядка включительно в некоторой окрестности точки
-го порядка включительно в некоторой окрестности точки  . Введём дифференциальный оператор
. Введём дифференциальный оператор
 .
.
Тогда разложением в ряд Тейлора функции  по степеням
по степеням  и
и  в окрестности точки
в окрестности точки  будет
будет

где  — остаточный член в форме Лагранжа:
— остаточный член в форме Лагранжа:

В случае функции одной переменной  , поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе
, поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе  .
.
· Пусть функция 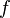 дифференцируема
дифференцируема  раз в точке
раз в точке  и
и  , а
, а  .
.
Если  чётно и
чётно и  , то
, то  - точка локального максимума. Если
- точка локального максимума. Если  чётно и
чётно и  , то
, то  - точка локального минимума. Если
- точка локального минимума. Если  нечётно, то экстремума нет.
нечётно, то экстремума нет.
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
 . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
|   
|
Итак, уравнение кривой имеет вид y = f(x). Обозначим  ординату касательной, соответствующую абсциссе x. Тогда
ординату касательной, соответствующую абсциссе x. Тогда  . Следовательно, разность ординат кривой и касательной при одном и том же значении xбудет
. Следовательно, разность ординат кривой и касательной при одном и том же значении xбудет  .
.
Разность f(x) – f(x0) преобразуем по теореме Лагранжа  , где c между x и x0.
, где c между x и x0.
Таким образом,
 .
.
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа:  , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
, где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
- Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,
 (x – x0) > 0 и (c – x0) > 0. Поэтому
(x – x0) > 0 и (c – x0) > 0. Поэтому  .
. - Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь
 .
.
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
 выпукла на [–1; 1].
выпукла на [–1; 1].