Классический метод

Расчет классическим методом производится по следующей методике.

1. Расчет схемы до коммутации с целью определения независимых начальных условий.

2. Расчет схемы после коммутации с целью определения установившихся составляющих токов и напряжений.

3. Составление характеристического уравнения. Наиболее простой способ этого - по входному комплексному сопротивлению относительно любой ветви. Желательно разорвать цепь в такой ветви, относительно которой выражение для Z _вх было бы проще. В выражении для Z _вх произведение jw заменяется на оператор р, а само выражение представляется в виде дроби, числитель которой приравнивается к нулю. Последнее равенство и является характеристическим уравнением.

4. Решение характеристического уравнения и запись формы общего решения для свободных составляющих токов или напряжений. При р_1,2 отрицательных действительных, например, для тока:

i _св = A₁e ^p1t + A ₂e ^p2t .

При р_1,2 =p кратных действительных отрицательных:

i _cв = (A ₁ + A ₂t) e ^pt .

При р_1,2 = -a ± jw_o ,т.е. комплексно-сопряженных:

i _св = А е ^-at (sin w₀t +y).

5. Запись переходных токов или напряжений :

i = i _уст + i _св , u = u _уст+ u _св

6. Расчет схемы после коммутации относительно зависимых начальных условий, т.е. при t = (0 ₊).

При этом i _L(0) = i _L(0_-) = i _L(0₊) ; u_C(0) = u_C(0_-) = u_C(0₊).

Для определения значения других токов и напряжений, а также их

производных при t = 0 составляется интегро-дифференциальная

система уравнений по законам Кирхгофа.

7. Определение постоянных интегрирования. Для этого записываются выражения для переходных токов или напряжений из п. 5 при t = 0 и выражения для их производных тоже при t = 0. Из полученной системы уравнений и находят неизвестные постоянные интегрирования.

8. Запись переходных токов и напряжений и проверка их при t = 0 и t = ¥.

9. Построение необходимых графиков.

Пример 1. E2

R ₁= R ₂ = R₃ = 10 Oм,

L = 10 мГн,

R1 C R3 С = 20 мкФ,

Е ₁ = 10 В,

Е ₂ = 20 В,

u _c , i _c, i _L ,i _R - ?

E1 R2 L

 

1. Расчет схемы до коммутации.

i1

i2 E2 R3 ì i ₁- i ₂ –i ₃ = 0;

R1 C Uc i3 íi₁R₁ +i₃R₃ +L =E₂ +E₁ ;

E1 R2 L

1 î i ₃R₃ – i ₂R₂ + L -u_c = E ₂ ;

i₂ = 0, т.к. i₂ = C 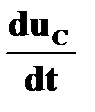= 0 (u_C = Const); i₁ = i₃ ;

L 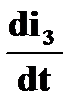= 0 , т.к. 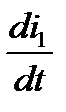=Сonst.

í i₁ = i₃ , í i₁( R₁+R₃ ) = E₂ + E₁,

í i₁ R₁ + i₃ R₃ = E₂ + E₁ , í i₃ R₃ – u_C = E₂.

í i₃ R₃ –u_C = E₂.

i₁ = 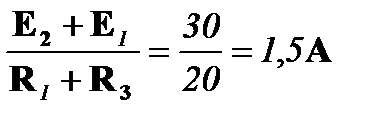; i₃ = 1,5 A;

u_C = i₃ R₃ – E₂ = 1,5 *10 – 20 = -5В .

Направление U_C и тока i₂ можно на схеме поменять на противоположное.

u_C( 0_-) = u_C( 0₊) = 5B; i₃ ( 0_-) = i₃( 0₊) = 1,5 A.

2. Расчет схемы после коммутации.

i1 E2

 

R1 C i2 Uc

 

i3

E1 R2 L ì i₁+ i₂ – i₃ = 0,

í i₁ R₁ + L = E₁ + E₂,

î i₂ R₂ + L + u_C = E₂.

i₂ = 0, L = 0 , i₁ = i_{3 ,}

i₁ R₁ = E₁ + E₂ , i₁ = i_1уст = , i_2уст = 0 .U _c=E ₂=U_{c уст}=20B

3. Составление характеристического уравнения.

 

R1 1/PC PL Z_вх(Р) = R₁ + =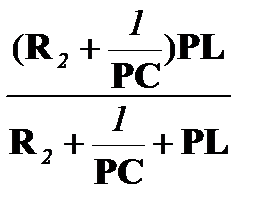

R2 = R₁ + =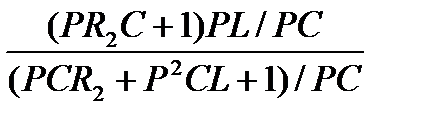

Zвх(Р)

 

= R₁ + ,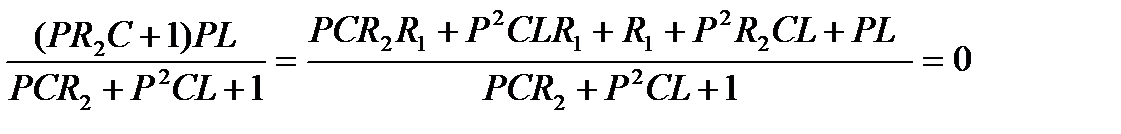

P²CL( R₁ + R₂ ) + P( CR₁R₂ +L ) +R₁ = 0.

4.Решение характеристического уравнения

P² *4*10^-6+P*12*10^-3+10=0;

P_1,2=(-12*10^-3

= -1,5*10³ j0,5*10³; = 1,5*10³ , w₀ =0,5*10³.

u_CCB = А е^{- t}sin ( ₀t + ).

5. u_C = u_{C уст} + u_C cв = 20 +А е^{- t} sin ( _ot + ).

i₂ = i_C = C = C( - Ae^{- t} sin ( _ot + ) + A _oe^{- t} cos ( _ot + )).

6. Определение зависимых начальных условий.

При t = 0 u_C (0) = 5B,

-- ? i₂(0) = C , = .

Для определения i₂(0) составляем уравнения по законам Кирхгофа при

t = 0 для схемы после коммутации.

æ i₁(0) + i₂(0) – i₃(0) = 0,

í i₁(0)R₁ +L(di₃(0)/dt) = E₁ + E₂ , (1)

î i₂(0)R₂ + L(di₃(0)/dt) + u_C(0) = E₂.

i₃(0) = 1,5 A, u_C(0) = 5B.

Решаем систему (1) относительно i₁(0), i₂(0), L(di₃(0)/dt) методом Гаусса.

 

1 1 0 1,5 1 1 0 1,5 1 1 0 1.5

10 0 1 30 ~ 0 -10 1 15 ~ 0 -10 1 15

0 10 1 15 0 10 1 15 0 0 2 30

 

L(di₃(0)/dt) = 30/2 = 15 B, i₂(0) = (15 –15)/(-10) = 0 , i₁(0) = 1,5 A.

7. Определение постоянных интегрирования.

u_C(0) = 20 + Asin = 5; ;

;

Asin ; - ; tg = ; ;

sin ; A= .

8. u_C(t) = 20 – 47,6e^-1500t sin(500t + 18,4^o);

Проверим:

u_C(0) = 20 –47,6 sin(18,4^o) = 5,

u_C( ;

i₂=C =

 

= -20*10^-6*47,6*500е^-1500t(3sin(500t+18,4^o)-1*cos(500t+18,4⁰)=

=0,476 =

=1,5e^-1500t sin (500t+18,4^o- )= 1,5e^-1500tsin500t;

tg = (1/ , .

Проверим i₂(0) = 1,5*sin(0^o)= 0;

i₂( ;

i₂(t) = 1,5e^-1500tsin500t (A).

Найдем ток i₃.

i₃ = i_{3 уст} + i_{3 св} , i_{3 св} = Me^-1500t sin(500t +b);

i₃ = 3 +Me^-1500t sin(500t + b) ; (2)

L . (3)

Далее находим производную от (2) и приравниваем её (3) при t=0.

В (2) подставляем t=0 и приравниваем i₃(0) из п.1. Из полученной системы определяем M и b аналогично определению u_C(t). Переходный ток i₁(t) определяем по закону Кирхгофа i₁(t) = i₃(t) – i₂(t).

9. Построим, например, график u_C(t).

 

 

-27.6

-15

Uc

t

Uc(t)

47,6 e-1500t