Общая постановка задачи оптимального управления.

 

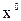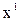В фазовом пространстве даны две точки и . Среди допустимых управлений u € U, переводящих фазовую точку из положения 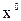в конечное положение 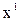(если такие управления есть) найти такое, для которого функционал

 

(1)

 

принимает наименьшее возможное значение.

t₁ – момент времени прохождения фазовой точки через конечную точку .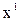

f₀ – функция f(x,u).

Функция f₀ определена и непрерывна вместе со своими частными

производными (j=1,..,n) на всем фазовом пространстве и

 

пространстве управления X×U.

 

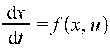Система называется автономной, т.к. правые ее части не

 

зависят явно от t. В противном случае система называется неавтономной:

 

 

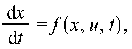
Время t определяется из условия x(t₁)=x¹.

Управление, дающее решение поставленной задачи, называется оптимальным.

Важным частным случаем задачи ОУ является задача об оптимальном быстродействии.

 

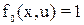
Для формулировки необходимого условия оптимальности удобно дать другую формулировку поставленной задачи. Добавим к фазовым координатам x₁,.., x_n ещё одну координату x⁰, закон изменения которой определяется ДУ:

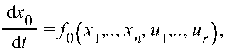
где - функция из (1).

 

Тогда рассматривается система дифференциальных уравнений, описывающих движение фазовой точки в (n+1)-мерном пространстве :

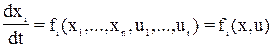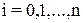, (2)

Обозначим через 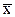вектор 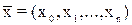или .

Система ДУ (2) будет иметь вид: .