Анализ задачи
Решение более или менее ответственных задач разумно начинать с анализа поставленной задачи. По этому вопросу имеется огромное количество источников, правда каждый из них ориентирован (явно или неявно) на специфику определенного класса рассматриваемых задач. В этом плане заслуживают внимания материалы проведенной в 2007 годунаучной конференции ТРИЗ-Саммит [62], где представлен достаточно широкий обзор подходов, показавших свою практическую эффективность при анализе изобретательских задач. Следование рекомендациям при рассмотрении таких сложных задач (с позиций потребности в интеллектуальных усилиях) - общепринято.
Для более же широкого класса задач методические рекомендации весьма общие и на практике (именно в силу их общности) им редко уделяют должное внимание: в простых случаях они как бы не важны сами по себе, в сложных ситуациях опытные исследователи фактически следуют им, сами не замечая этого (они как бы сами собой разумеются). Задача состоит в том, чтобы обратить на них внимание начинающих и научить разумно их использовать в каждой конкретной ситуации своей профессиональной деятельности. Ведь, по-существу, уже на этапе анализа поставленной задачи начинается процесс ее решения и заключается он в снятии ряда неопределенностей, которые обычно присутствуют в исходной постановке. Дело в том, что появление задачи – есть констатация наличия некоторой неопределенности между тем, что дано и тем, что требуется определить. Снятие этой неопределенности и является, по-существу, целью решения задачи, и этот процесс начинается еще на этапе уяснения задачи. Уже здесь, в частности, определяется сфера доминирования (какая область и какие ее аспекты рассматриваются), обеспечивается единство языка постановки задачи и рассматриваемой предметной области (уже здесь часто необходима интерпретация используемых терминов) и другие.
В ходе уяснения задачи, как минимум приходится реализовать следующие шаги. Во-первых, необходимо уяснить: понятны ли в данном контексте использованные в постановке термины и язык в целом. К сожалению, под одними и теми же терминами очень часто понимаются разные объекты. Поэтому будет полезным обращение к соответствующим словарям (тезаурусам) и современным базовым работам по данной тематике. Следует уточнить, о каком именно объекте идет речь, и какова точка зрения, с которой он рассматривается, что также будет способствовать адекватному пониманию использованной лексики.
Во-вторых, проводится уяснение цели: что же по существу требуется найти. Следует помнить, что цель данной системе формулируется в надсистеме и в ее интересах. Типичным является случай, когда вместо определения значений некоторых параметров, обеспечивающих экстремальное значение критерия, целью обозначается поиск его экстремального значения. Например, в задаче о построении оптимального по прибыли плана целью иногда называют величину наибольшей прибыли, вместо того, чтобы искать пути (план) достижения этой прибыли.
В-третьих, уточнение заданных условий. Речь идет об интерпретации приведенного описания, возможных уточнениях и предположениях, которые в тексте задания заданы неявно или недостаточно четко обозначены. Более того, в целом ряде случаев субъект вынужден самостоятельно принять и зафиксировать дополнительные ограничения или допущения необозначенные в постановке, например: «потерями в линии электропередачи пренебрегаем» или «зависимость параметра 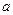 от параметра
от параметра 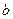 принимается линейной», «трение воздуха не учитываем» и т.п. Именно в выявление реально существующих связей между элементами системы и в последующей их формализации лежит ключ к успеху решения большинства задач математического моделирования.
принимается линейной», «трение воздуха не учитываем» и т.п. Именно в выявление реально существующих связей между элементами системы и в последующей их формализации лежит ключ к успеху решения большинства задач математического моделирования.
Первое, что приходит в голову после анализа рассматриваемой задачи, решалась ли такая задача ранее. В настоящее время этот этап в значительной мере реализуется в результате поиски соответствующей информации с помощью Интернет. Однако, и в этом случае каждый раз реализуется один из следующих случаев [63]:
· задача новая, ранее не в такой форме не рассматривалась;
· задача формулировалась, но решение не получено;
· задача решалась и решена, но при несколько иных условиях и допущениях;
· задача решена, причем может иметь несколько решений.
В каждой из этих ситуаций приходится действовать несколько по-разному. Проблемным, правда, всегда остается вопрос о полноте проведенного поиска (никогда нет уверенности в том, что ситуация именно такая). Но в реальной действительности когда-то прекратить поиск все же приходится, следует классифицировать сложившуюся ситуацию и предпринимать соответствующие дальнейшие действия.
В процессе анализа задачи существенную помощь может оказать классификация постановок задач. Приведем, следуя [64], описание наиболее характерных типов постановок задач.
Постановка типа A.
Цель решения задачи - нахождение одного из допустимых вариантов решения. Каждое решение X допустимо, если отвечает некоторой совокупности внутренне сбалансированных и непротиворечивых целевых ограничений и ограничений по ресурсам. Цели здесь могут выражаться в виде специальных ограничений типа "быть не менее чем..." или твердых заданий "быть равным ...". Они лишь косвенно выражают приоритет вариантов и направление устремлений. Например, требуется сформировать учебный план неполной средней школы. В рамках этой проблемы может быть задана следующая задача: за восемь первых лет обучения в школе на математику необходимо выделить не менее 1500 часов учебного времени и непременно изучить методы решения квадратных уравнений за 20 часов.
Математическая запись такого рода постановок может быть следующей: определить 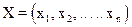 при ограничениях
при ограничениях
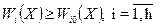 - целевые ограничения,
- целевые ограничения,
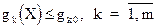 - ресурсные ограничения.
- ресурсные ограничения.
Результатами формализации постановок типа А являются: модели прямого вычисления (вычисления по формулам, решение систем уравнений и неравенств), модели баланса, модели прогнозирования и др, что позволяет получать оценки некоторых характеристик, описывать состояние и поведение объектов исследования.
Постановки типа B.
Эти постановки формулируются как требование максимизации (минимизации) некоторых характеристик объекта исследования, которые выступают в качестве критериев оценки и отбора вариантов. Цель - определить некоторую совокупность показателей 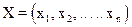 обеспечивающую экстремальное значение критериальной функции (поэтому задачи, имеющие постановку такого типа, называются оптимизационными). Множество допустимых вариантов решения задается системой ограничений, как требование принадлежности некоторому допустимому множеству D. Таким образом, математическая запись постановок задач типа В может быть следующей:
обеспечивающую экстремальное значение критериальной функции (поэтому задачи, имеющие постановку такого типа, называются оптимизационными). Множество допустимых вариантов решения задается системой ограничений, как требование принадлежности некоторому допустимому множеству D. Таким образом, математическая запись постановок задач типа В может быть следующей:
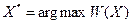 ½
½ 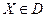
или
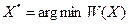 ½
½ 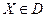 ,
,
где  – целевая функция;
– целевая функция; 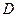 –область допустимых решений.
–область допустимых решений.
Подобные математические модели предписывают норму поведения объекта и относятся к моделям нормативного типа. Решив подобную математическую задачу, получают вполне определенный и наилучший в смысле принятого критерия план действий.
return false">ссылка скрытаЕсли требования экстремизации относится к нескольким характеристикам, то говорят о векторной (многокритериальной) оптимизации. Например, требуется разработать план подготовки в условиях заочного обучения (D) за самый короткий срок (T) специалистов с наивысшим в данной области образованием V и с наименьшими затратами средств W, т.е.

Однако вся совокупность этих требования, как правило, противоречива, а с математической точки зрения их одновременное выполнение абсурдно. Так явно противоречивы требования минимизации сроков и затрат при подготовке специалистов наивысшего качества. Существуют различные приемы изменения противоречивых постановок с целью их дальнейшей формализации и применения математических методов решения задачи, однако прямое решение задач многокритериальной оптимизации наталкивается на принципиальные трудности.
Постановка типа C.
Это наиболее общий вид задач поиска решения встречающийся в целенаправленной деятельности людей. В постановках такого типа дают развернутую формулировку целей и обычно не привязываются к структуре выделяемых ресурсов. Цели могут последовательно конкретизироваться вплоть до введения целевых нормативов (как в постановках типа B), однако цели и критерии в этом типе постановок разделены. Тогда оценка качества решения осуществляется путем вычисления отклонения выбранных показателей от этих нормативов. Если же интересующие показатели просто перечислены, то постановка становится похожей на постановку типа A. Целевые нормативы могут быть как-то ранжированы или даже взвешены. В последнем случае постановка C внешне будет походить на постановку типа B. Постановки задач тапа С претендуют на высшую степень адекватности, однако нахождение их эффективных решений - дело будущего.
Сравнивая типы постановок, можно сказать следующее. Постановки типа A обычно предназначены только для решения вопросов анализа и прогноза. Постановки типа В приводят к весьма жестким моделям, правда решение в этом случае получается наилучшим в смысле принятых критериев и ограничений. Разделение целей и критериев оценки вариантов решений в постановках типа C позволяет получать более гибкие модели способные адаптироваться к существенным изменениям условий задачи.
Примечание. Как всегда на практике, чаще всего встречаются некоторые гибриды такого рода схем, и приходится, либо с целью подгонки под какую-то схему вводить в постановку задачи некоторые дополнительные условия (или уточнять свою интерпретацию), либо мучительно формировать собственный подход к ее решению. Здесь важно понимать, что каждую задачу в данной форме кто-то сформулировал. Поэтому как именно поставлена задача, а, следовательно, и какие использовать для ее решения методы моделирования зависит от исследователя, его целей, знаний и возможностей. В этой связи следует различать ситуации, когда формирование (обсуждение, корректировка) постановки задачи и ее решение строго разделены или связаны между собой, в том числе и обратной связью.
Приведем два простейших примера.
Задача 1. Определить дальность полета предмета, выпущенного под известным углом  к поверхности земли с заданной начальной скоростью
к поверхности земли с заданной начальной скоростью 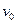 .
.
Проанализируем эту задачу. Поскольку иной информации в задании нет, то будем предполагать идеальный случай: поверхность земли плоская, предмет летит в плоскости перпендикулярной поверхности, сопротивление воздуха не учитывается, размерами предмета можно пренебречь, предмет выпущен с уровня земли (все эти предположения непосредственно не следуют из постановки задачи и приняты нами, как дополнительные). Предмет брошен по некоторым углом, поэтому его движение, осуществляемое по некоторой траектории, удобно представить в виде разложения на два слагаемых: на горизонтальное движение и движение вертикальное. Заметим, что нам требуется определить расстояние, которое пролетит предмет по горизонтали.
При сделанных предположениях горизонтальное движение (в соответствии с первым законом Ньютона) есть прямолинейное движение с постоянной скоростью. Поэтому за время 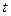 по горизонтали предмет пролетит расстояние
по горизонтали предмет пролетит расстояние  . Если считать, что предмет брошен в момент времени
. Если считать, что предмет брошен в момент времени 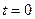 , то это расстояние есть величина
, то это расстояние есть величина 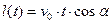 Эта формула показывает, что движение в горизонтальном направлении может продолжаться сколь угодно долго. Однако этого не происходит, почему?
Эта формула показывает, что движение в горизонтальном направлении может продолжаться сколь угодно долго. Однако этого не происходит, почему?
Мы можем наблюдать, что вначале предмет поднимается на некоторую высоту, а затем падает вниз. Когда он достигнет уровня земли, то, очевидно, закончится его движение и в горизонтальном направлении. Таким образом, предмет продолжает свое движение в горизонтальном направлении только до тех пор, пока он не опустится на землю (обозначим время полета через 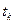 ). Следовательно, предмет пролетит расстояние
). Следовательно, предмет пролетит расстояние 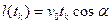 . Задача будет решена, если найдем время приземления предмета
. Задача будет решена, если найдем время приземления предмета 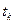 (остальные компоненты
(остальные компоненты 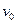 и
и 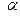 заданы).
заданы).
В вертикальном направлении движение предмета определяют две составляющие: восходящий вертикальный компонент броска направленный вверх и нисходящий компонент, обусловленный силой тяжести. Пролетаемое расстояние вверх (по аналогии с горизонтальной составляющей) описывается формулой  ). Поэтому за время
). Поэтому за время 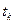 предмет мог бы пройти расстояние
предмет мог бы пройти расстояние  .
.
Движение вниз является равноускоренным (движение свободного падения), поэтому за время 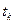 , предмет мог бы пролететь вниз расстояние
, предмет мог бы пролететь вниз расстояние  . Предполагается, что предмет выпущен с уровня земли и закончит свое движение на этом же уровне. В этой связи в любой момент времени
. Предполагается, что предмет выпущен с уровня земли и закончит свое движение на этом же уровне. В этой связи в любой момент времени 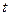 выполняется условие
выполняется условие 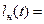
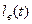 или
или 
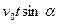 . Отсюда можно найти время полета предмета
. Отсюда можно найти время полета предмета 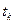 . Оно равно
. Оно равно  . За это время в горизонтальном направлении предмет пролетит искомое расстояние
. За это время в горизонтальном направлении предмет пролетит искомое расстояние  .
.
Решение удалось получить в общем виде – искомая величина связана с заданными параметрами по формуле  . Эта формула может рассматриваться, как математическая модель протяженности движения предмета, подброшенного под углом к горизонту (правда при сделанных допущениях). Следовательно, она справедлива при различных значениях возможных параметров. Именно в этом сила получаемых аналитических решений, подставляя соответствующие значения параметров, получаем решение соответствующей задачи. Например, если угол бросания равен
. Эта формула может рассматриваться, как математическая модель протяженности движения предмета, подброшенного под углом к горизонту (правда при сделанных допущениях). Следовательно, она справедлива при различных значениях возможных параметров. Именно в этом сила получаемых аналитических решений, подставляя соответствующие значения параметров, получаем решение соответствующей задачи. Например, если угол бросания равен  и начальная скорость
и начальная скорость  , то предмет пролетит расстояние
, то предмет пролетит расстояние  (где ускорение свободного падения
(где ускорение свободного падения 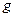 принято равным
принято равным  ).
).
Задача 2. Проектируется канал оросительный системы, имеющий прямоугольное сечение площадью  . Каковы должны быть размеры сечения, чтобы для облицовки стен и дна канала потребовалось наименьшее количество облицовочного материала?
. Каковы должны быть размеры сечения, чтобы для облицовки стен и дна канала потребовалось наименьшее количество облицовочного материала?
По-видимому (это первое наше предположение), количество требующегося облицовочного материала (обозначим его через  ) пропорционально некоторому коэффициенту
) пропорционально некоторому коэффициенту  , определяющему расход материала на единицу площади, и суммарной площади (стен и дна) канала
, определяющему расход материала на единицу площади, и суммарной площади (стен и дна) канала 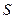 , т.е.
, т.е.  . В постановке явно не указано, но можно предположить (это второе наше предположение), что сечение канала одинаково на всем его протяжении. Поэтому подлежащая облицовке площадь равна произведению длины канала
. В постановке явно не указано, но можно предположить (это второе наше предположение), что сечение канала одинаково на всем его протяжении. Поэтому подлежащая облицовке площадь равна произведению длины канала  и длине периметра его сечения. Следовательно,
и длине периметра его сечения. Следовательно,  , где
, где 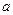 - высота,
- высота, 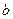 - ширина сечения канала – искомые величины. Именно изменение этих величин и позволяет (в соответствии с условиями задачи) менять объем облицовочного материала. Стремление минимизировать расход облицовочного материала запишем в следующем виде
- ширина сечения канала – искомые величины. Именно изменение этих величин и позволяет (в соответствии с условиями задачи) менять объем облицовочного материала. Стремление минимизировать расход облицовочного материала запишем в следующем виде

В соответствии с постановкой задачи сечение канала представляет собой прямоугольник с площадью  . Эти сведения позволяют связать размеры его сторон следующим образом
. Эти сведения позволяют связать размеры его сторон следующим образом  . В итоге проведенные рассуждения приводят к следующей задаче:
. В итоге проведенные рассуждения приводят к следующей задаче:
определить значения параметров 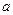 и
и 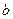 при условиях
при условиях
 (1)
(1)
 (2)
(2)
если  (3).
(3).
В данном случае условие (3) - третье наше предположение - кажется тривиальным, однако оно не является лишним, и в более сложных задачах такого типа условия могут играть принципиальную роль.
Сравним формулировку задачи (1) - (3) с исходной. Если последняя есть задача, сформулированная на естественном языке (и является, по-существу, вербальной моделью), то запись (1)-(3) является чисто математической задачей и может рассматриваться как математическая модель нормативного типа.
Ход решения такого типа математической задачи должен быть известен даже школьникам. Используя (2), выразим параметр 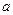 через
через 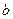 , т.е.
, т.е.  и подставим его в (1). Имеем
и подставим его в (1). Имеем

или
 (4)
(4)
Для определения значений параметра  , при котором выполняется условие (4) необходимо продифференцировать
, при котором выполняется условие (4) необходимо продифференцировать  по
по 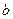 (именно этот параметр варьируется), и полученный результат приравнять нулю. В итоге для нахождения
(именно этот параметр варьируется), и полученный результат приравнять нулю. В итоге для нахождения 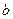 получаем следующее уравнение
получаем следующее уравнение  . Единственное, физически реализуемое решение которого, есть
. Единственное, физически реализуемое решение которого, есть  . Таким образом, ответом задачи являются значения следующие размеры прямоугольного сечения: высота
. Таким образом, ответом задачи являются значения следующие размеры прямоугольного сечения: высота  и ширина
и ширина  .
.