Интерполяция
Аппроксимирующей функцией является полином Лагранжа. В качестве координат сигнала обычно предпочитают его отсчеты  . Для построения интерполяционного полинома n-ой степени нужно иметь
. Для построения интерполяционного полинома n-ой степени нужно иметь  отсчет, т.е.
отсчет, т.е.  . Моменты времени
. Моменты времени  , k=0,1,...,n называют узлами интерполяции.
, k=0,1,...,n называют узлами интерполяции.
Общая картина интерполяции полиномом n-й степени представлена на рис.2.75).

Рис.2.75
Здесь  – i-й участок интерполяции;
– i-й участок интерполяции;  – i-й интервал между координатами сигнала;
– i-й интервал между координатами сигнала;  – узлы интерполяции;
– узлы интерполяции;  – текущая погрешность интерполяции(аппроксимации) на i-м участке.
– текущая погрешность интерполяции(аппроксимации) на i-м участке.
В общем случае интервал между отсчетами сигнала (узлами)  . Если интервал
. Если интервал  , то на участке аппроксимации узлы интерполяции равноотстоящие. Для равноотстоящих узлов
, то на участке аппроксимации узлы интерполяции равноотстоящие. Для равноотстоящих узлов  .
.
Задача интерполяции формулируется таким образом. Пусть задан  отсчет
отсчет  в узлах
в узлах  , k=0,1,...,n. Требуется найти аппроксимирующий полином
, k=0,1,...,n. Требуется найти аппроксимирующий полином  , проходящий через все отсчеты в узлах интерполяции.
, проходящий через все отсчеты в узлах интерполяции.
Решением данной задачи является интерполяционный полином Лагранжа. Возможны две формы записи полинома Лагранжа. Они отличаются видом координат сигнала.
1) Первая форма. Здесь координаты – это коэффициенты разложения  функции
функции  в ряд по базису
в ряд по базису  .
.
В этом случае полином Лагранжа имеет вид
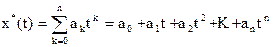 ,
,
где коэффициенты 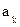 определяются решением системы
определяются решением системы 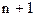 уравнений
уравнений
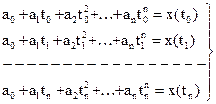 система уравнений.
система уравнений.
2) Вторая форма. Здесь координаты – это 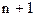 отсчет сигнала. Данная форма наиболее удобна и широко распространена в измерительной технике.
отсчет сигнала. Данная форма наиболее удобна и широко распространена в измерительной технике.
В этом случаеполином Лагранжа имеет вид
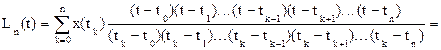
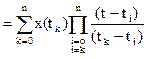 .
.
Очевидно, при 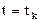 имеем
имеем  , т. е. полином Лагранжа совпадает с функцией
, т. е. полином Лагранжа совпадает с функцией  в узлах интерполяции.
в узлах интерполяции.
Исходя из остаточного члена полинома,максимальнаяпогрешность интерполяции при равномерном критерии приближения
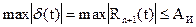 ,
,
где 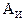 – оценка сверху остаточного члена
– оценка сверху остаточного члена 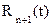 интерполяционного полинома Лагранжа,
интерполяционного полинома Лагранжа,
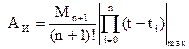 .
.
Для равноотстоящих узлов
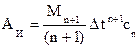 ,
,
где  ;
; 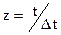 .
.