Решение задач линейного программирования графическим методом

 

Задача линейного программирования (ЛП) в общем виде формулируется следующим образом.

Для переменных x₁ ,…, x_j ,…, x_n найти такие неотрицательные значения x_j ³ 0 , ,которые обращали бы в максимум целевую функцию

, (1)

и удовлетворяли системе ограничений

. (2)

Для удобства геометрического представления основной задачи линейного программирования рассматривается случай, когда число переменных n на 2 больше числа уравнений m, т. е. n–m=2. Это означает, что две переменные можно взять в качестве свободных, например x₁ , x₂, а остальные сделать базисными и выразить их через свободные. Получится система ограничений вида

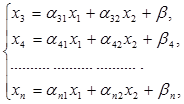
(3)

 

где a_ij – пересчитанные коэффициенты матрицы системы,

b_i – правые части ограничений.

 

Свободные переменные можно взять в качестве осей координат; x₁ , x₂ ³ 0, следовательно, графическое решение будет находиться в первом квадранте координатной плоскости (x₁ , x₂). Остальные базисные переменные также должны удовлетворять требованию неотрицательности x₃ ³ 0, x₄ ³ 0, …, x_n ³ 0. Это означает, что если взять предельное значение равенства нулю, например x₃ = 0, то из системы (3) следует, что это будет в выбранной системе координат уравнение прямой a₃₁ x₁ + a₃₂ x₂ + b₃ = 0.

При этом по одну сторону от прямой будет полуплоскость,в которой x₃ < 0, а по другую - x₃ >0, что соответствует требованию неотрицательности. Интересующую полуплоскость переменной x₃ = 0 удобно отметить штриховкой, как это показано на рис.1. Аналогично можно построить и остальные прямые: x₄ = 0, …, x_n = 0 с выделением штриховкой допустимой стороны.

В результате часть плоскости, принадлежащая всем полуплоскостям, образует область допустимых решений (ОДР), представляющую собой выпуклый многоугольник. Если хотя бы одна из полуплоскостей не перекрывает область допустимых решений, как, например, x_j на рис.1, то задача не имеет решения.

 

Теперь необходимо рассмотреть графическое нахождение из числа допустимых решений оптимального решения, обращающего в максимум или в минимум (в зависимости от условий задачи) целевую функцию (2), приводимую здесь в развернутом виде:

F_max = c₁ x₁ +…+ c_j x_j +…+ c_n x_n .

Подставив в указанную формулу значения базисных переменных, выраженных через свободные (3), получим линейную функцию, зависящую только от свободных переменных с возможным свободным членом g₀ :

F = g₁ x₁ + g₂ x₂ + g₀ . (4)

Данное уравнение можно построить в тех же координатах, что и область допустимых решений. Очевидно, наклон полученной прямой будет определяться величинами и знаками коэффициентов g₁ и g₂ . От величины g₀ будет зависеть смещение этой прямой относительно начала координат.Для предварительного построения прямой, соответствующей целевой функции (4), можно выбрать произвольное значение g₀ , которое в процессе графического решения задачи все равно будет изменяться. Остается определить направление сдвига рассматриваемой прямой для оптимизации функционала.

Если коэффициенты положительны, т. е. g₁ >0 , g₂ >0, то из (4) следует, что, например, для максимизации надо перемещать прямую целевой функции в сторону увеличения x₁ , x₂ (вправо и вверх) до тех пор, пока она не достигнет крайних значений границы области допустимых решений, как показано на рис. 2. Значения координат этой точки и будут оптимальными значениями x₁⁰ , x₂⁰.

 

Для вычисления значений остальных переменных оптимальные значения x₁⁰ , x₂⁰ подставляются в систему (3).

Также вычисляется оптимальное значение целевой функции

.

 

В случае других знаков коэффициентов направления перемещения максимизируемой целевой функции приведены на рис. 3.

Графический метод решения применим для случая двух свободных переменных, уже при трех свободных переменных его использование затруднено.