Базис и размерность линейного подпространства

 

Ранее было определено понятие подпространства и установлено, что подпространство в свою очередь является пространством.

Для подпространства сохраняют смысл понятия полноты, линейной независимости,

базиса и размерности.

25°. Если E 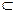V (подпространство), то dimE ≤ dimV.

◀ Линейно зависимый набор в E будет таковым и в V, поэтому максимальное количество линейно независимых векторов в E не превышает максимального количества линейно независимых векторов в V. ▶

26°. Если E 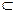V и dimE = dimV, то E ≡ V. Доказать самостоятельно.

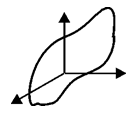Базис подпространства всегда можно дополнить до базиса пространства, но (как иллюстрирует картинка) из данного базиса пространства не всегда можно выделить базис подпространства.

27°. Линейная оболочка ℒ 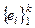является подпространством и dimℒ ≤ k.

Доказать самостоятельно.

28°. Линейная оболочка ℒ 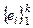– подпространство, натянутое на 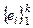– это наименьшее подпространство, содержащее эти векторы. Доказать самостоятельно.